What Is Regression Testing Types Of Regression Testing When To Perform

What Is Regression Testing Types Of Regression Testing When To Perform With linear regression with no constraints, r2 r 2 must be positive (or zero) and equals the square of the correlation coefficient, r r. a negative r2 r 2 is only possible with linear regression when either the intercept or the slope are constrained so that the "best fit" line (given the constraint) fits worse than a horizontal line. I was just wondering why regression problems are called "regression" problems. what is the story behind the name? one definition for regression: "relapse to a less perfect or developed state.".

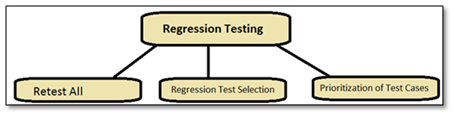
What Is Regression Testing Types Need Techniques And Tools Reqtest Q&a for people interested in statistics, machine learning, data analysis, data mining, and data visualization. The pearson correlation coefficient of x and y is the same, whether you compute pearson(x, y) or pearson(y, x). this suggests that doing a linear regression of y given x or x given y should be the. Is it possible to have a (multiple) regression equation with two or more dependent variables? sure, you could run two separate regression equations, one for each dv, but that doesn't seem like it. For the top set of points, the red ones, the regression line is the best possible regression line that also passes through the origin. it just happens that that regression line is worse than using a horizontal line, and hence gives a negative r squared. undefined r squared.

Regression Testing Ensuring Smooth Software Evolution Is it possible to have a (multiple) regression equation with two or more dependent variables? sure, you could run two separate regression equations, one for each dv, but that doesn't seem like it. For the top set of points, the red ones, the regression line is the best possible regression line that also passes through the origin. it just happens that that regression line is worse than using a horizontal line, and hence gives a negative r squared. undefined r squared. The biggest challenge this presents from a purely practical point of view is that, when used in regression models where predictions are a key model output, transformations of the dependent variable, y hat, are subject to potentially significant retransformation bias. 8 i've published a method for identifying outliers in nonlinear regression, and it can be also used when fitting a linear model. hj motulsky and re brown. detecting outliers when fitting data with nonlinear regression – a new method based on robust nonlinear regression and the false discovery rate. bmc bioinformatics 2006, 7:123. A good residual vs fitted plot has three characteristics: the residuals "bounce randomly" around the 0 line. this suggests that the assumption that the relationship is linear is reasonable. the res. Where β∗ β ∗ are the estimators from the regression run on the standardized variables and β^ β ^ is the same estimator converted back to the original scale, sy s y is the sample standard deviation of the regressand, and sx s x is the sample standard deviation. unfortunately the book doesn't cover the analogous result for multiple.

Regression Testing Types Learn The Various Types Of Regression Testing The biggest challenge this presents from a purely practical point of view is that, when used in regression models where predictions are a key model output, transformations of the dependent variable, y hat, are subject to potentially significant retransformation bias. 8 i've published a method for identifying outliers in nonlinear regression, and it can be also used when fitting a linear model. hj motulsky and re brown. detecting outliers when fitting data with nonlinear regression – a new method based on robust nonlinear regression and the false discovery rate. bmc bioinformatics 2006, 7:123. A good residual vs fitted plot has three characteristics: the residuals "bounce randomly" around the 0 line. this suggests that the assumption that the relationship is linear is reasonable. the res. Where β∗ β ∗ are the estimators from the regression run on the standardized variables and β^ β ^ is the same estimator converted back to the original scale, sy s y is the sample standard deviation of the regressand, and sx s x is the sample standard deviation. unfortunately the book doesn't cover the analogous result for multiple.