Trigonometric Functions Of Any Angle Unit Circle Radians Degrees Coterminal Reference Angles

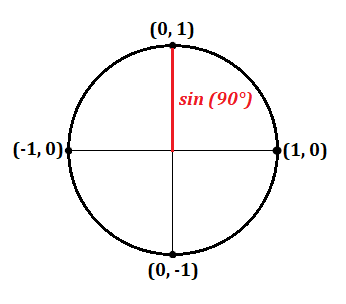
3 Expert Tips For Using The Unit Circle This trigonometry video tutorial explains how to evaluate trigonometric functions of any angle such as acute angles or special angles. it shows you how to find and use reference. Identified are special angles, given in both degrees and radians, that give exact trigonometric values. the points on the unit circle associated with a given angle can be used to calculate the trigonometric values as cos θ = x and sin θ = y for an angle θ and point (x, y).

Trigonometry On The Unit Circle Angles In Both Degrees And Radians (iii) converting between degree and radian measure example: change each degree measure to radians, each radian measure to degrees and sketch angle in standard position. Measuring angles in radians has other applications besides calculating arclength, and we will need to evaluate trigonometric functions of angles in radians. the sine, cosine, or tangent of a particular angle is the same whether the angle is measured in radians or in degrees. This section develops the trigonometric functions based on angle measurement and relates it to the concept of the circular or wrapping function developed previously, which relied on movement around the perimeter of a unit circle. Use ordered pairs on the unit circle to determine trig function values. use calculators to find trig function values. reference angles are formed between the terminal side of an angel and the closest part of the x axis. consider the angle 150 ∘.

Trigonometric Functions Of Any Angle Unit Circle Rationale This section develops the trigonometric functions based on angle measurement and relates it to the concept of the circular or wrapping function developed previously, which relied on movement around the perimeter of a unit circle. Use ordered pairs on the unit circle to determine trig function values. use calculators to find trig function values. reference angles are formed between the terminal side of an angel and the closest part of the x axis. consider the angle 150 ∘. Master the unit circle with this comprehensive guide! learn angles, radians, coordinates, and trigonometric functions with ease. Using the unit circle, we are able to apply trigonometric functions to any angle, including those greater than [latex]90^ {\circ} [ latex]. the unit circle demonstrates the periodicity of trigonometric functions by showing that they result in a repeated set of values at regular intervals. Right triangle trigonometry in this lesson you learned how to evaluate trigonometric functions of acute angles and how to use the fundamental trigonometric identities. Thus, to convert from radians to degrees, we can multiply by. a unit circle is a circle with a radius of 1, and it is used to show certain common angles. unit circle: commonly encountered angles measured in radians and degrees. radians to degrees. is the length of the curve along the arc.