Total Time Complexity Test Total Time Complexity Heap Sort Array

Array Time Complexity Pdf Heap sort is a comparison based sorting algorithm that uses a binary heap data structure. it works by first building a max heap (or min heap) from the input array and then repeatedly extracting the maximum (or minimum) element from the heap to build the sorted array. Time complexity analysis: heapify a single node takes o (log n) time complexity where n is the total number of nodes. therefore, building the entire heap will take n heapify operations and the total time complexity will be o (n*logn).

Time Complexity Of Building A Heap Heap Prepbytes Blog When the heap is stored in an array (rather than dynamic tree nodes with pointers), then we can build the heap bottom up, i.e., starting from the leaves and up to the root, then using amortized analysis we can get total time complexity of o (n), whereas we cannot empty the heap minima's bottom up. In this article, we have explained time & space complexity of heap sort with detailed analysis of different cases like worst case, best case and average case. Step 1: build a max heap from array has n elements. time = heapify (n) = log (n) step 2: replace it with the last item of the heap followed by reducing the size of the heap by 1. finally, heapify the root of the tree. time = log (n) heapify (n 1) = log (n) log (n 1) step 3: repeat step 2 while the size of the heap is greater than 1. Sort an array given an array of integers nums, sort the array in ascending order and return it. you must solve the problem without using any built in functions in o (nlog (n)) time complexity and with the smallest space complexity possible.

Heap Sort Time Complexity Time Complexity Sorting Complex Step 1: build a max heap from array has n elements. time = heapify (n) = log (n) step 2: replace it with the last item of the heap followed by reducing the size of the heap by 1. finally, heapify the root of the tree. time = log (n) heapify (n 1) = log (n) log (n 1) step 3: repeat step 2 while the size of the heap is greater than 1. Sort an array given an array of integers nums, sort the array in ascending order and return it. you must solve the problem without using any built in functions in o (nlog (n)) time complexity and with the smallest space complexity possible. Heap sort is a comparison based sorting algorithm that converts an array into a heap data structure and repeatedly extracts the largest (or smallest) element to sort the array. Efficient time complexity: heap sort has a time complexity of o (n log n) in all cases. this makes it efficient for sorting large datasets. the log n factor comes from the height of the binary heap, and it ensures that the algorithm maintains good performance even with a large number of elements. Heap sort is a fundamental sorting algorithm used in data structures. it efficiently organizes elements into a sorted sequence by using the properties of a binary heap. Both the time complexity for building heap and heap sort is added and gives us the resultant complexity as nlogn. hence, the total time complexity is of the order of [big theta]: o(nlogn). the worst case time complexity is [big o]: o(nlogn). the best case time complexity is [big omega]: o(nlogn).

Heap Sort With Example Time Complexity Cs Taleem Heap sort is a comparison based sorting algorithm that converts an array into a heap data structure and repeatedly extracts the largest (or smallest) element to sort the array. Efficient time complexity: heap sort has a time complexity of o (n log n) in all cases. this makes it efficient for sorting large datasets. the log n factor comes from the height of the binary heap, and it ensures that the algorithm maintains good performance even with a large number of elements. Heap sort is a fundamental sorting algorithm used in data structures. it efficiently organizes elements into a sorted sequence by using the properties of a binary heap. Both the time complexity for building heap and heap sort is added and gives us the resultant complexity as nlogn. hence, the total time complexity is of the order of [big theta]: o(nlogn). the worst case time complexity is [big o]: o(nlogn). the best case time complexity is [big omega]: o(nlogn).
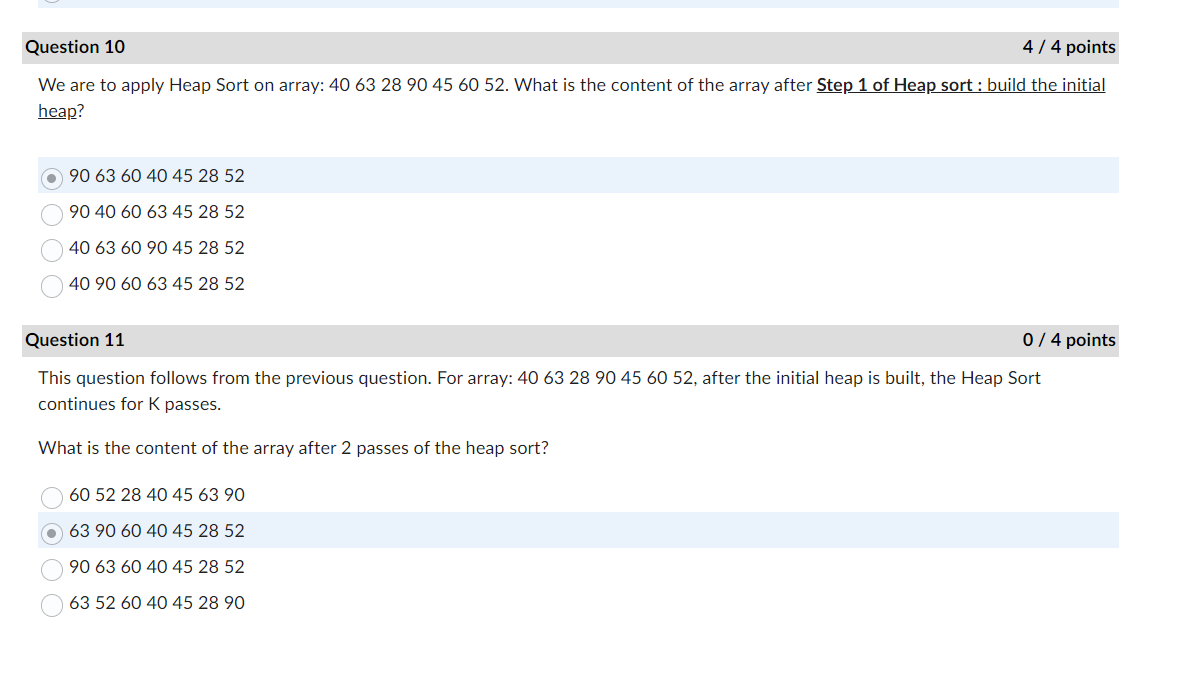
Solved We Are To Apply Heap Sort On Array 406328904560 52 Chegg Heap sort is a fundamental sorting algorithm used in data structures. it efficiently organizes elements into a sorted sequence by using the properties of a binary heap. Both the time complexity for building heap and heap sort is added and gives us the resultant complexity as nlogn. hence, the total time complexity is of the order of [big theta]: o(nlogn). the worst case time complexity is [big o]: o(nlogn). the best case time complexity is [big omega]: o(nlogn).

Time Complexity Of Inserting Into A Heap Baeldung On Computer Science
Comments are closed.