Spatial Dependence In A Regression Model

Geodata Spatial Regression 5 Detecting Spatial Dependence Traditional regression models assume that each observation is independent of others, which is rarely the case in spatial data. these models take spatial dependency into account for the modeling process, making them powerful tools for analyzing data where location matters. Spatial regression deals with the specification, estimation, and diagnostic checking of regression models that incorporate spatial effects. two broad classes of spatial effects may be distinguished, referred to as spatial dependence and spatial heterogeneity (anselin, 1988b).
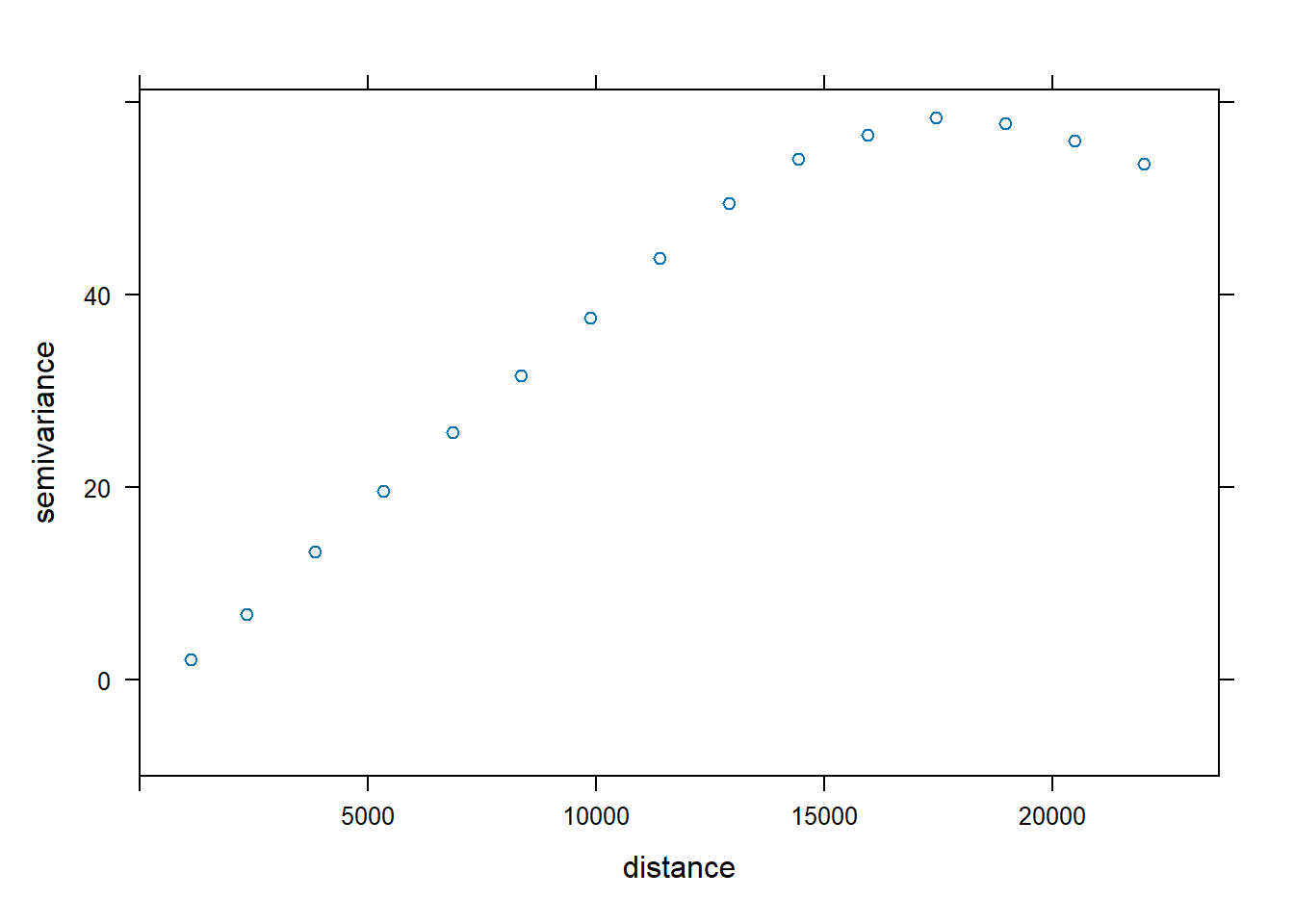
Geodata Spatial Regression 5 Detecting Spatial Dependence There are various techniques to model spatial dependence and spatial processes (lesage and pace 2009). here, we will just cover a few of the most common techniques econometric models. Regression is a modeling paradigm in which we specify a mathematical relationship between independent and dependent variables. a regression includes a deterministic model to specify the average behavior. it specifies a stochastic model to describe the variability around the average behavior. what is the dual model paradigm?. Central limit theorems are developed for instrumental variables estimates of linear and semi parametric partly linear regression models for spatial data. general forms of spatial dependence and heterogeneity in explanatory variables and unobservable disturbances are permitted. Spatial linear regression (slr) model with spatial error (se) dependence, or the se model in short, takes the following form: where the se structure is a spatial autoregressive (sar) process. it can also be a spatial moving average (sma) process: un = ρwn n n, β: k × 1 vector of regression coefficients. durbin se model.
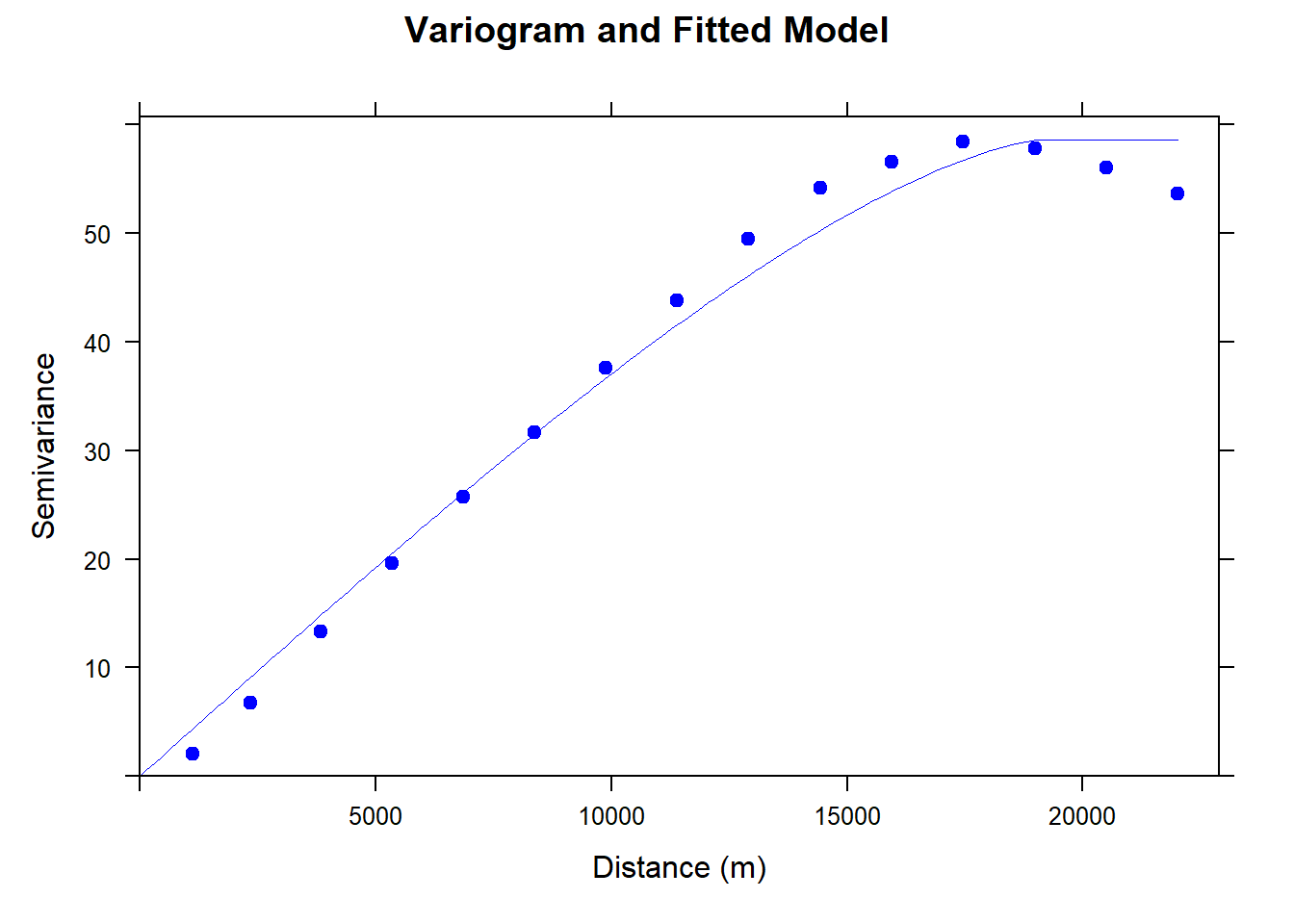
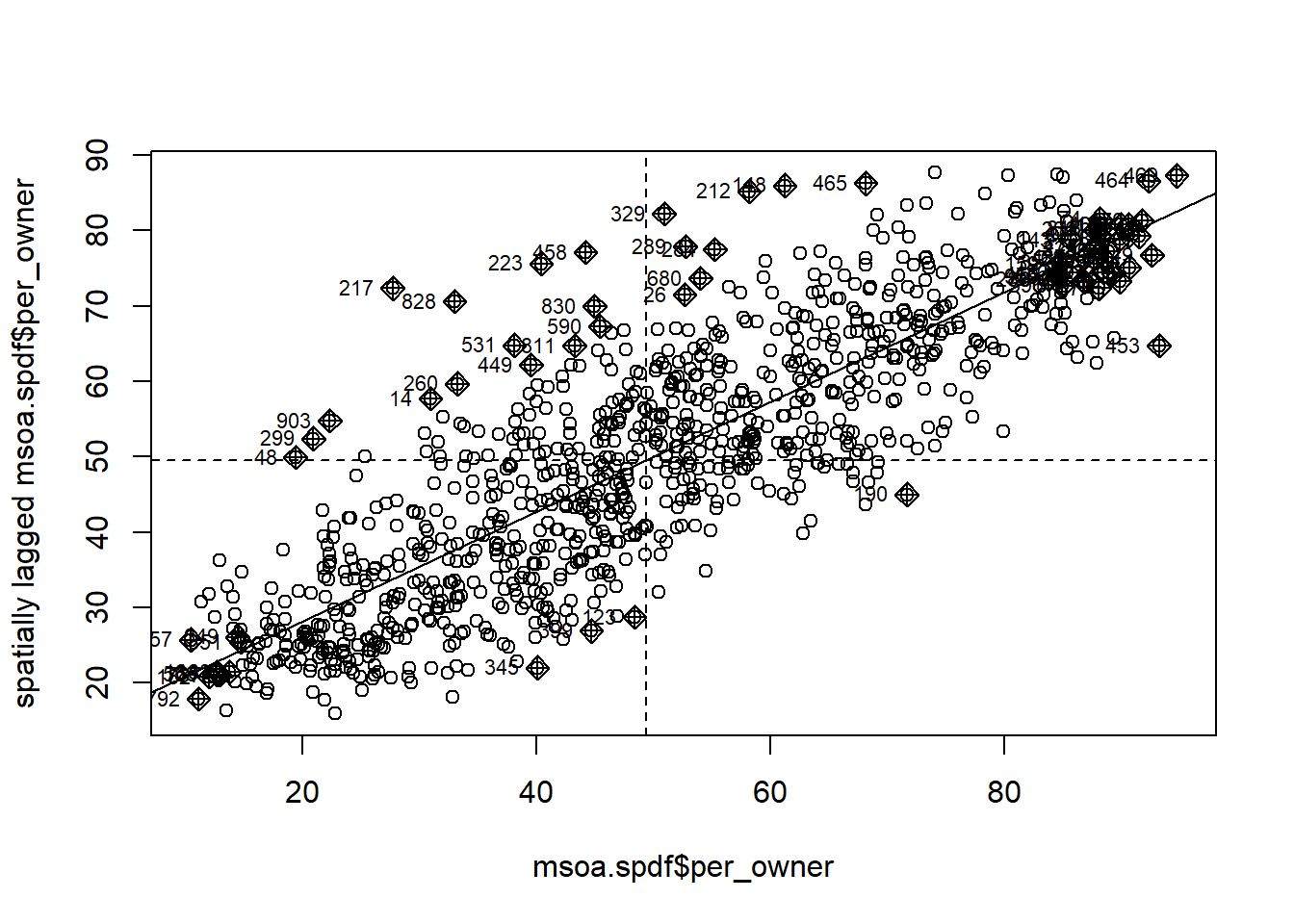
Geodata Spatial Regression 5 Detecting Spatial Dependence Central limit theorems are developed for instrumental variables estimates of linear and semi parametric partly linear regression models for spatial data. general forms of spatial dependence and heterogeneity in explanatory variables and unobservable disturbances are permitted. Spatial linear regression (slr) model with spatial error (se) dependence, or the se model in short, takes the following form: where the se structure is a spatial autoregressive (sar) process. it can also be a spatial moving average (sma) process: un = ρwn n n, β: k × 1 vector of regression coefficients. durbin se model. From there, we formalize space and spatial relationships in three main ways: first, encoding it in exogenous variables; second, through spatial heterogeneity, or as systematic variation of outcomes across space; third, as dependence, or through the effect associated to the characteristics of spatial neighbors. In this lab guide, we formally incorporate spatial dependency between units of observations in a regression framework. we will be closely following this week’s handout on spatial regression. the objectives of this lab are as follows. learn how to decide between a standard linear regression, spatial lag, and spatial error model. Spatial dependence is measured by spatial autocorrelation, which is a property of data that arises whenever there is a spatial pattern in the values, as opposed to a random pattern that indicates no spatial autocorrelation. this spatial pattern can be measured through standard global and local spatial statistics. Multiplying any variable vector x with the spatial weights matrix w produces the `spatially lagged' variable vector. for each unit i (each row), the spatially lagged variable vector wx contains the spatially weighted values of the neighbouring units (as de ned by w ).
Geodata Spatial Regression 5 Detecting Spatial Dependence From there, we formalize space and spatial relationships in three main ways: first, encoding it in exogenous variables; second, through spatial heterogeneity, or as systematic variation of outcomes across space; third, as dependence, or through the effect associated to the characteristics of spatial neighbors. In this lab guide, we formally incorporate spatial dependency between units of observations in a regression framework. we will be closely following this week’s handout on spatial regression. the objectives of this lab are as follows. learn how to decide between a standard linear regression, spatial lag, and spatial error model. Spatial dependence is measured by spatial autocorrelation, which is a property of data that arises whenever there is a spatial pattern in the values, as opposed to a random pattern that indicates no spatial autocorrelation. this spatial pattern can be measured through standard global and local spatial statistics. Multiplying any variable vector x with the spatial weights matrix w produces the `spatially lagged' variable vector. for each unit i (each row), the spatially lagged variable vector wx contains the spatially weighted values of the neighbouring units (as de ned by w ).
Geodata Spatial Regression 5 Detecting Spatial Dependence Spatial dependence is measured by spatial autocorrelation, which is a property of data that arises whenever there is a spatial pattern in the values, as opposed to a random pattern that indicates no spatial autocorrelation. this spatial pattern can be measured through standard global and local spatial statistics. Multiplying any variable vector x with the spatial weights matrix w produces the `spatially lagged' variable vector. for each unit i (each row), the spatially lagged variable vector wx contains the spatially weighted values of the neighbouring units (as de ned by w ).

Geodata Spatial Regression 5 Detecting Spatial Dependence
Comments are closed.