Space Complexity Of Recursive Algorithms Solved Problem 1

Space Complexity Of Algorithms Pdf Computing Algorithms Algorithms: space complexity of recursive algorithms (solved problem 1) topics discussed: 1. finding the space complexity of recursive algorithms .more. To generalize, a recursive function's memory complexity is o (recursion depth). as our tree depth suggests, we will have n total return statements and thus the memory complexity is o (n)." but does that mean all recursive calls have o (n) space complexity? (function always returns only once right?) here's how i think about it:.

Free Video Space Complexity Of Recursive Algorithms Solved Problem 1 The amount of memory required by the algorithm to solve given problem is called space complexity of the algorithm. the space complexity of an algorithm quantifies the amount of space taken by an algorithm to run as a function of the length of the input. Explore the intricacies of space complexity in recursive algorithms through a solved problem in this 10 minute educational video. dive into the process of determining space complexity for recursive algorithms, focusing on a specific example. Public static void main(string[] args) { count = 0; double[] a = { 1, 2, 3, 4, 5}; system.out.println("sum is " rsum(a, a.length)); system.out.println("count is " count); } } we can convert any iterative program to recursive. Space complexity: however, it requires additional space proportional to the size of the input array for the merge operation, resulting in o(n)o(n) space complexity.

Space Complexity Of Recursive Function Public static void main(string[] args) { count = 0; double[] a = { 1, 2, 3, 4, 5}; system.out.println("sum is " rsum(a, a.length)); system.out.println("count is " count); } } we can convert any iterative program to recursive. Space complexity: however, it requires additional space proportional to the size of the input array for the merge operation, resulting in o(n)o(n) space complexity. For instance, take a typical "calculate factorial using recursion" function: int fact(int x) { if (x > 1) { return x * fact(x 1); } else { return 1; } } it says the time complexity is o (n) and the space complexity is o (n). all well and good. next, change the to a . it still says the time and space complexities are both o (n). Practise problems on time complexity of an algorithm 1. analyse the number of instructions executed in the following recursive algorithm for computing nth fibonacci numbers as a function of n public static int fib(int n) { if(n==0) return 1; else if(n==1) return 1; else return(fib(n 1) fib(n 2));. In this article, we’ll delve deeper into the analysis of time and space complexity in recursive algorithms by examining two classic examples: calculating the fibonacci sequence and binary. How to calculate space complexity of different algorithms (recursive, divide and conquer, greedy, etc.) (with examples) 1. recursive algorithms: list the data structures and variables utilized in each recursive call.

Chapter 1b Complexity For Recursive Algorithms Pdf For instance, take a typical "calculate factorial using recursion" function: int fact(int x) { if (x > 1) { return x * fact(x 1); } else { return 1; } } it says the time complexity is o (n) and the space complexity is o (n). all well and good. next, change the to a . it still says the time and space complexities are both o (n). Practise problems on time complexity of an algorithm 1. analyse the number of instructions executed in the following recursive algorithm for computing nth fibonacci numbers as a function of n public static int fib(int n) { if(n==0) return 1; else if(n==1) return 1; else return(fib(n 1) fib(n 2));. In this article, we’ll delve deeper into the analysis of time and space complexity in recursive algorithms by examining two classic examples: calculating the fibonacci sequence and binary. How to calculate space complexity of different algorithms (recursive, divide and conquer, greedy, etc.) (with examples) 1. recursive algorithms: list the data structures and variables utilized in each recursive call.
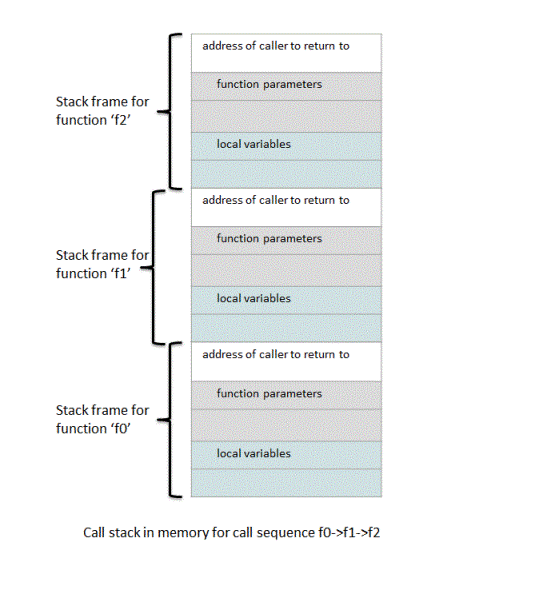
Time And Space Complexity Of Recursive Algorithms Ideserve In this article, we’ll delve deeper into the analysis of time and space complexity in recursive algorithms by examining two classic examples: calculating the fibonacci sequence and binary. How to calculate space complexity of different algorithms (recursive, divide and conquer, greedy, etc.) (with examples) 1. recursive algorithms: list the data structures and variables utilized in each recursive call.

Time And Space Complexity Of Recursive Algorithms Ideserve
Comments are closed.