Sorted List To Balanced Binary Search Tree Sorted Linked List To Bst

Convert A Sorted Doubly Linked List To Balanced Binary Search Tree Given a singly linked list which has data members sorted in ascending order. construct a balanced binary search tree which has same data members as the given linked list. Convert sorted list to binary search tree given the head of a singly linked list where elements are sorted in ascending order, convert it to a height balanced binary search tree.

Convert A Sorted Doubly Linked List To Balanced Binary Search Tree What's the best way to create a balanced binary search tree from a sorted singly linked list? a few questions: do you know the number of elements in the sll? how about creating nodes bottom up? this solution's time complexity is o (n). detailed explanation in my blog post: leetcode 2010 11 convert sorted list to balanced binary . In this tutorial, we’ll discuss creating a balanced binary search tree (bst) from a sorted list. firstly, we’ll explain the meaning of balanced binary search trees. then, we’ll discuss the top down and bottom up approaches and compare them. 2. balanced binary seach tree. in the beginning, let’s define the meaning of balanced binary search trees. Given the head of a singly linked list where elements are sorted in ascending order, convert it to a height balanced bst. for this problem, a height balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1. In this article, we will implement a balanced binary search tree (bst) from a sorted linked list. a binary tree is considered balanced if the height of the left subtree and the height of the right subtree of every node differ by no more than 1.

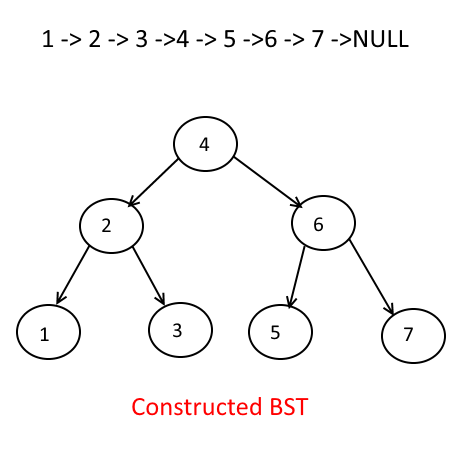
Convert Sorted Singly Linked List To Balanced Binary Search Tree Given the head of a singly linked list where elements are sorted in ascending order, convert it to a height balanced bst. for this problem, a height balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1. In this article, we will implement a balanced binary search tree (bst) from a sorted linked list. a binary tree is considered balanced if the height of the left subtree and the height of the right subtree of every node differ by no more than 1. In this blog, we discussed the approach for converting a sorted linked list to a balanced bst (binary search tree). in a balanced bst, the difference between the height of the left subtree and the right subtree should not be greater than one. We can create a binary search tree with the list by just creating a skew tree, where we will just put the list nodes as a right child only. for example, let's say the sorted list is: 1 >2 >3 >4 >5. then the skew tree that can be created from this would be:. To convert a sorted singly linked list to a height balanced binary search tree (bst), we will use the recursive approach. the key idea is to find the middle element of the linked list, make it the root of the bst, and then recursively do the same for the left and right halves of the linked list. The problem presents a singly linked list sorted in ascending order and asks us to convert it into a height balanced binary search tree (bst). a height balanced binary tree is one where the depth of the two subtrees of every node never differs by more than one.