Solving Recurrence Relation Using Recursion Tree Method

Recursion Tree Method Pdf Recurrence Relation Mathematical Logic Steps to solve recurrence relation using recursion tree method: calculate the cost at each level and count the total no of levels in the recursion tree. note: if summing up all the levels becomes complex, we can find an upper bound by considering a perfectly full tree and or an infinite geometrical series (the ratio is typically less than 1). A recursion tree is a tree where each node represents the cost of a certain recursive sub problem. we will follow the following steps for solving recurrence relations using recursion tree method.
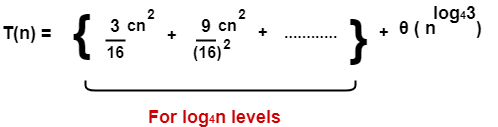
Solving Recurrences Using Recursion Tree Method Gate Vidyalay A recursion tree is a tree where each node represents the cost of a certain recursive sub problem. then you can sum up the numbers in each node to get the cost of the entire algorithm. A recursion tree is useful for visualizing what happens when a recurrence is iterated. it diagrams the tree of recursive calls and the amount of work done at each call. 1 solving recurrences expanding the recurrence into a tree summing the cost at each level applying the substitution method an example consider the recurrence relation t (n 3t n 4 cn2 ) = ( ) for some constant c . Express the tc of the algorithm as a recurrence formula. e.g.: f(n) = n f(n 1) expand it to a summation with no recursive term. find a concise expression (or upper bound), e(n), for the summation. find ,ideally, or o (big oh) for e(n). compute the number of nodes in certain trees.
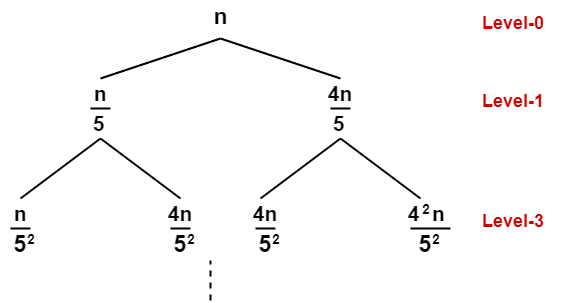
Recursion Tree Method For Solving Recurrences Examples Ppt Gate Vidyalay 1 solving recurrences expanding the recurrence into a tree summing the cost at each level applying the substitution method an example consider the recurrence relation t (n 3t n 4 cn2 ) = ( ) for some constant c . Express the tc of the algorithm as a recurrence formula. e.g.: f(n) = n f(n 1) expand it to a summation with no recursive term. find a concise expression (or upper bound), e(n), for the summation. find ,ideally, or o (big oh) for e(n). compute the number of nodes in certain trees. Traversing a recursion tree provides insights into the execution flow of a recursive function. starting from the initial call at the root node, we follow the branches to reach subsequent calls until we encounter the base case. There are several methods for solving recurrence relations (see clrs 4.3 { 4.5 for details). we will mainly use the recursion tree method. this is a two step strategy for solving recurrence relations: construct a recursion tree by unwinding the recurrence relation. determine the cost of the entire tree by summing the costs of the nodes. There are mainly three steps in the recursion tree method. in this section, we will learn each of them one by one. construct a recursion tree from the recurrence relation at hand. find the total number of levels in the recursion tree. compute the cost of each level in the tree. Use a recursion tree to determine a good asymptotic upper bound on the recurrence t (n) = 4 t (n 2 2) n t (n)= 4t (n 2 2) n. use the substitution method to verify your answer.

Solved 2 Recurrence Relation Using Recursion Tree Iteration Chegg Traversing a recursion tree provides insights into the execution flow of a recursive function. starting from the initial call at the root node, we follow the branches to reach subsequent calls until we encounter the base case. There are several methods for solving recurrence relations (see clrs 4.3 { 4.5 for details). we will mainly use the recursion tree method. this is a two step strategy for solving recurrence relations: construct a recursion tree by unwinding the recurrence relation. determine the cost of the entire tree by summing the costs of the nodes. There are mainly three steps in the recursion tree method. in this section, we will learn each of them one by one. construct a recursion tree from the recurrence relation at hand. find the total number of levels in the recursion tree. compute the cost of each level in the tree. Use a recursion tree to determine a good asymptotic upper bound on the recurrence t (n) = 4 t (n 2 2) n t (n)= 4t (n 2 2) n. use the substitution method to verify your answer.
Algorithms Solve The Recurrence Using Recursion Tree Method There are mainly three steps in the recursion tree method. in this section, we will learn each of them one by one. construct a recursion tree from the recurrence relation at hand. find the total number of levels in the recursion tree. compute the cost of each level in the tree. Use a recursion tree to determine a good asymptotic upper bound on the recurrence t (n) = 4 t (n 2 2) n t (n)= 4t (n 2 2) n. use the substitution method to verify your answer.
Comments are closed.