Solved What Would Be The Output Of The Following Algorithm Chegg

Solved What Output Is Produced By The Following Algorithm Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. here’s the best way to solve it. refer to the image attached for detaile … not the question you’re looking for? post any question and get expert help quickly. answer to what is the output of the following algorithm?. Which of the following operations performed by an algorithm would most likely use both selection and iteration? determine the number of cards with the suit equal to hearts. compute the average value of the cards. determine the number of cards in the hand. compute the sum of the cards' value.
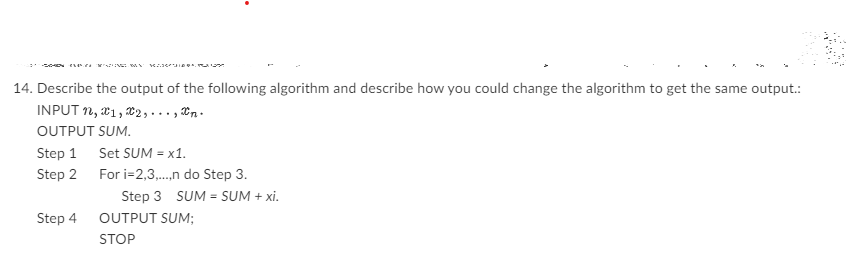
Solved 14 Describe The Output Of The Following Algorithm Chegg You'd like to output a two dimensional n by n array b in which b [i, j] (for i < j) contains the sum of array entries a [i] through a [j] that is, the sum a [i] a [i 1] a [j]. (the value of array entry b [i, j] is left unspecified whenever i >= j, so it doesn't matter what is output for these values.). Video answer: okay for a problem. three. they ask us what is the output for the variable total after a segment of code executes? well, let's see, they made numb and total imagers on. so let's see, they set numb is. The algorithm suggests that t(n) = t(i) t(n − 1 − i) 1. by summing this relationship for all the possible random values i = 0, 1, . . . , n − 1, we obtain that in average nt(n) = 2(t(0) t(1) . . . t(n−2) t(n−1)) n. 1. lots of ones (20 points) how many ones does the following procedure print when run with input n? compute the best bounds you can: the exact value if possible, a big Θ expression if you can’t find the exact value, or big o and big Ω bounds if you can’t find a big Θ expression. ones(n): if n = 0: print 1 else: for i = 1 to 2^n: ones(n 1).
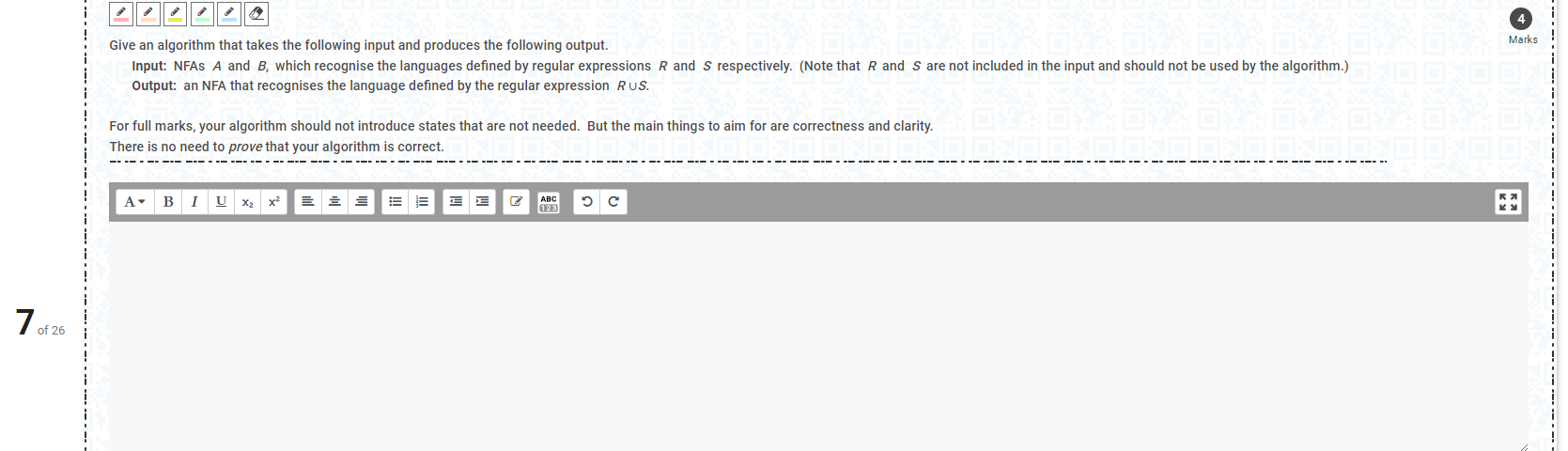
Give An Algorithm That Takes The Following Input And Chegg The algorithm suggests that t(n) = t(i) t(n − 1 − i) 1. by summing this relationship for all the possible random values i = 0, 1, . . . , n − 1, we obtain that in average nt(n) = 2(t(0) t(1) . . . t(n−2) t(n−1)) n. 1. lots of ones (20 points) how many ones does the following procedure print when run with input n? compute the best bounds you can: the exact value if possible, a big Θ expression if you can’t find the exact value, or big o and big Ω bounds if you can’t find a big Θ expression. ones(n): if n = 0: print 1 else: for i = 1 to 2^n: ones(n 1). Et p (x) = x3 x 1 will design an algorithm to solve the polynomial multiplication problem. in particular, the input to the problem for input size n ≥ 1 are the co ef icients of the two polynomials p0, . . . , pn−1 and q0, . . . , qn−1. the output should be the coefficient r0, . . , r2n−2, where p (x) = pn−1 pi ixi, q(x) = pn. Engineering computer science computer science questions and answers what is the growth rate of the following algorithm, in terms of the input \ ( n \) ``` for i := 1 to n for j := 1 to i a := 7*i j next j next i ``` for simplicity, please only include what would be inside the big theta: \ ( \theta ( [ \) your answer \ ( ]) \). Which of the following statements are true of algorithms? choose all that apply. a. they must be written in computer code. b. they provide step by step instructions. c. they break complex tasks into manageable steps. d. they are the basis for much teaching and learning. e. they are used in a computer program to solve a problem. b. To solve, either: top down: record subproblem solutions in a memo and re use (recursion memoization) bottom up: solve subproblems in topological sort order (usually via loops) for fibonacci, n 1 subproblems (vertices) and < 2n dependencies (edges) time to compute is then o(n) additions # recursive solution (top down) def fib(n):.
Comments are closed.