Solved Use Principle Of Mathematical Induction To Prove That Chegg

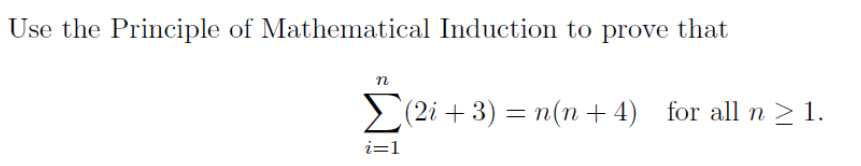
Solved Use The Principle Of Mathematical Induction To Prove Chegg Use the principle of mathematical induction to prove that: 1 2^2 <= 3^n for all positive integer 𝑛. your solution’s ready to go! enhanced with ai, our expert help has broken down your problem into an easy to learn solution you can count on. Compute x20. use an extended principle of mathematical induction in order to show that for n 1, n = use the result of part (b) to compute x20.

Solved Use The Principle Of Mathematical Induction To Prove Chegg Mathematical induction (or weak mathematical induction) is a method to prove or establish mathematical statements, propositions, theorems, or formulas for all natural numbers ‘n ≥1.’. it involves two steps: base step: it proves whether a statement is true for the initial value (n), usually the smallest natural number in consideration. Using the principle to proof by mathematical induction we need to follow the techniques and steps exactly as shown. we note that a prove by mathematical induction consists of three steps. • step 1. (basis) show that p (n₀) is true. • step 2. (inductive hypothesis). To prove that a statement p (n) is true for all integers , n ≥ 0, we use the principle of math induction. the process has two core steps: basis step: prove that p (0) is true. inductive step: assume that p (k) is true for some value of k ≥ 0 and show that p (k 1) is true. video answer. Worksheet 5.1 mathematical induction sitive integers n, wherep (n) is a propo base step: we verify that p (1) is true. inductive step: we show that the conditional statement p (k) ! p (k 1) is true for all positive integers k:.

Use The Principle Of Mathematical Induction To Prove Chegg To prove that a statement p (n) is true for all integers , n ≥ 0, we use the principle of math induction. the process has two core steps: basis step: prove that p (0) is true. inductive step: assume that p (k) is true for some value of k ≥ 0 and show that p (k 1) is true. video answer. Worksheet 5.1 mathematical induction sitive integers n, wherep (n) is a propo base step: we verify that p (1) is true. inductive step: we show that the conditional statement p (k) ! p (k 1) is true for all positive integers k:. 1, k=1 and 2n x 1 = 2n − 2. k=3 the principle of mathematical induction is used to establish the truth of a sequence of statements or formula which depend . n a natural number, n = 1, 2, . . we will use pk to stan. for a statement which depends on k. for example, pk might stand for the statem. nt “the number 2k − 1 is . dd.” these st. Ex 4.1,2: prove the following by using the principle of mathematical induction 13 23 33 n3 = ( ( 1) 2)^2 let p (n) : 13 23 33 43 n3 = ( ( 1) 2)^2 for n = 1, l.h.s = 13 = 1 r.h.s = (1 (1 1) 2)^2= ( (1 2) 2)^2= (1)2 = 1 hence, l.h.s. = r.h.s p (n) is true f. The principle of mathematical induction is a fundamental concept in mathematics used to prove statements about natural numbers. it is typically used to prove statements of the form "p (n)" for all natural numbers "n". In this mathematics article, we will learn the concept of mathematical induction, the statement of principle of mathematical induction, how to prove by mathematical induction, strong induction, reverse induction, and solve problems based on mathematical induction.

Use The Principle Of Mathematical Induction To Prove Chegg 1, k=1 and 2n x 1 = 2n − 2. k=3 the principle of mathematical induction is used to establish the truth of a sequence of statements or formula which depend . n a natural number, n = 1, 2, . . we will use pk to stan. for a statement which depends on k. for example, pk might stand for the statem. nt “the number 2k − 1 is . dd.” these st. Ex 4.1,2: prove the following by using the principle of mathematical induction 13 23 33 n3 = ( ( 1) 2)^2 let p (n) : 13 23 33 43 n3 = ( ( 1) 2)^2 for n = 1, l.h.s = 13 = 1 r.h.s = (1 (1 1) 2)^2= ( (1 2) 2)^2= (1)2 = 1 hence, l.h.s. = r.h.s p (n) is true f. The principle of mathematical induction is a fundamental concept in mathematics used to prove statements about natural numbers. it is typically used to prove statements of the form "p (n)" for all natural numbers "n". In this mathematics article, we will learn the concept of mathematical induction, the statement of principle of mathematical induction, how to prove by mathematical induction, strong induction, reverse induction, and solve problems based on mathematical induction.

Solved Use The Principle Of Mathematical Induction To Prove Chegg The principle of mathematical induction is a fundamental concept in mathematics used to prove statements about natural numbers. it is typically used to prove statements of the form "p (n)" for all natural numbers "n". In this mathematics article, we will learn the concept of mathematical induction, the statement of principle of mathematical induction, how to prove by mathematical induction, strong induction, reverse induction, and solve problems based on mathematical induction.