Solved The Method Of Ordinary Least Squares Also Known Chegg

Solved The Method Of Ordinary Least Squares Also Known Chegg Enhanced with ai, our expert help has broken down your problem into an easy to learn solution you can count on. the method of "ordinary least squares," also known as "the least squares method," does which of the following?read carefully. sse = ∑ i = 1 n (y i x i) 2. here’s the best way to solve it. The ordinary least squares (ols) method is a statistical technique used in linear regression to estimate the parameters (coefficients) of a linear model that best fits a set of data points.

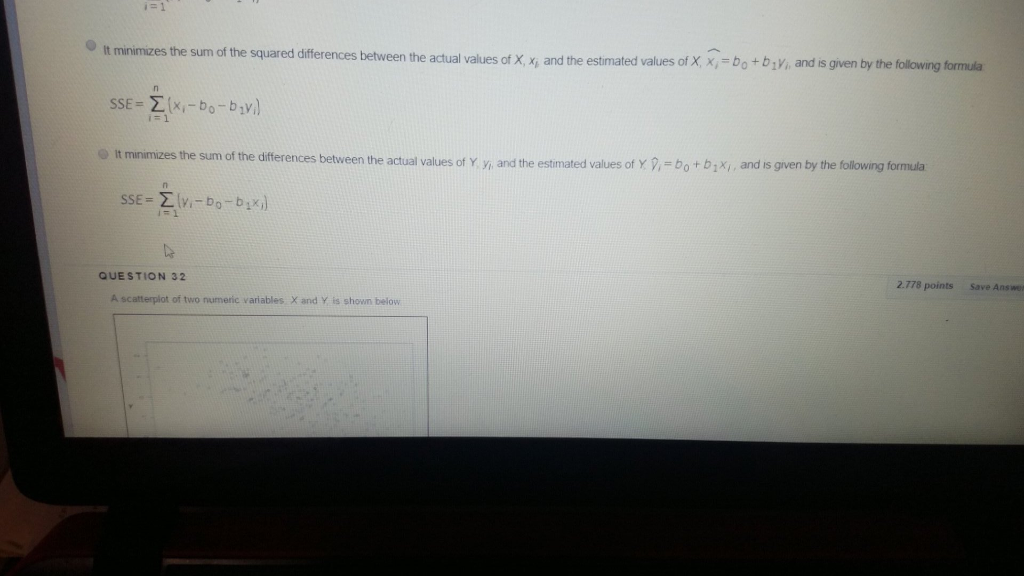
Solved The Method Of Ordinary Least Squares Also Known Chegg Method of least squares can be used to determine the line of best fit in such cases. it determines the line of best fit for given observed data by minimizing the sum of the squares of the vertical deviations from each data point to the line. Ordinary least squares (ols) is a technique used in linear regression model to find the best fitting line for a set of data points by minimizing the residuals (the differences between the observed and predicted values). It minimizes the sum of the differences between the actual values of y, yi, and the estimated values of y, y with hat on top subscript i equals b subscript 0 plus b subscript 1 x subscript i , and is given by the following formula: s s e equals sum from i equals 1 to n of open parentheses y subscript i minus b subscript 0 minus b subscript 1 x s. We will present two methods for finding least squares solutions, and we will give several applications to best fit problems. we begin by clarifying exactly what we will mean by a “best approximate solution” to an inconsistent matrix equation.

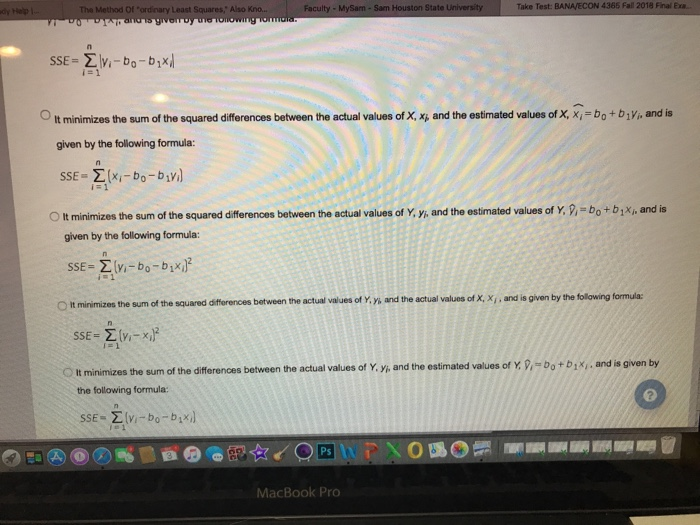
Solved The Method Of Ordinary Least Squares Also Known As Chegg It minimizes the sum of the differences between the actual values of y, yi, and the estimated values of y, y with hat on top subscript i equals b subscript 0 plus b subscript 1 x subscript i , and is given by the following formula: s s e equals sum from i equals 1 to n of open parentheses y subscript i minus b subscript 0 minus b subscript 1 x s. We will present two methods for finding least squares solutions, and we will give several applications to best fit problems. we begin by clarifying exactly what we will mean by a “best approximate solution” to an inconsistent matrix equation. I = 1, . . . , n (25) with e( i) = 0 for all i and also n ≥ p. , . . . , {xip}, i = 1, . . . , n? the principle of least squares chooses as estimates of θ1, θ2, . . . , � p those values ˆθ1, n x s(θ1, θ2, . . . , θp) = {yi − θ1xi1 − θ2xi2 − . . . − θpxip}2 (26). In statistics, this model loss is called ordinary least squares (ols). the solution to ols is the minimizing loss for parameters θ ^, also called the least squares estimate. we now know how to generate a single prediction from multiple observed features. Ordinary least squares the model: y = xb e where y and e are column vectors of length n (the number of observations), x is a matrix of dimensions n by k (k is the number of parameters), and b is a column vector of length k. for every observation i = 1;2;:::;n, we have the equation yi = xi1b1 xikbk ei. To perform ordinary least square method, you do the following steps: set a difference between dependent variable and its estimation: square the difference: take summation for all data to get the parameters that make the sum of square difference become minimum, take partial derivative for each parameter and equate it with zero, for example:.