Solved The Bellman Ford Algorithm Is Run On The Following Chegg

Solved B Bellman Ford Run Bellman Ford Algorithm On The Chegg The bellman ford algorithm is run on the following graph. the start vertex is a. assume each loop of the algorithm visits vertices in the graph in the following order: a, b, c, d. fill in each vertex's values after the third iteration. there are 3 steps to solve this one. Approach: bellman ford algorithm o (v*e) time and o (v) space. a negative weight cycle is a cycle in a graph, whose sum of edge weights is negative. if you traverse the cycle, the total weight accumulated would be less than zero.

Solved B Bellman Ford Run Bellman Ford Algorithm On The Chegg Run the bellman ford algorithm on the directed graph of figure 24.4, using vertex z z as the source. in each pass, relax edges in the same order as in the figure, and show the d d and \pi π values after each pass. The bellman ford algorithm is one of the first algorithms to find the shortest path between a source and all other vertices in a digraph without negative cycles. Finding the longest simple path in a graph with non negative edge weights is an np hard problem, for which no known polynomial time algorithm exists. suppose one simply negates each of the edge weights and runs bellman ford to compute shortest paths. Shortest paths and cheapest paths this applet presents the bellman ford algorithm, which calculates shortest paths even when cost can be negative. what do you want to do first? test the algorithm! read a detailed description of the algorithm.
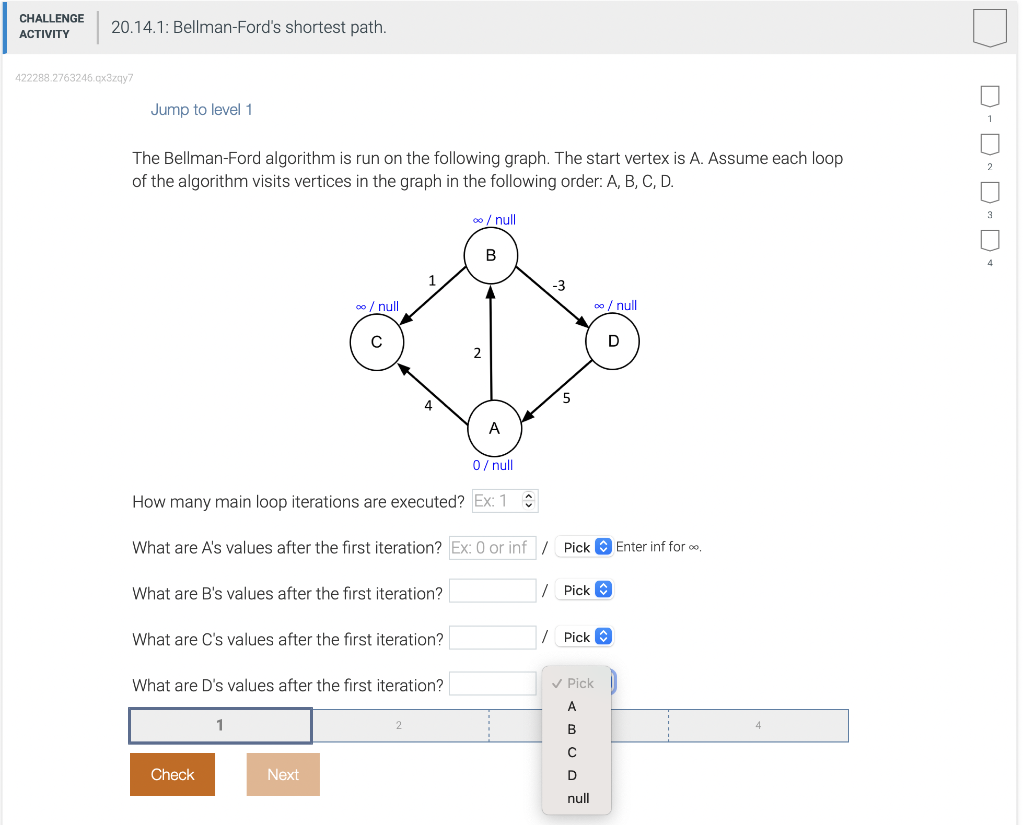
Solved The Bellman Ford Algorithm Is Run On The Following Chegg Finding the longest simple path in a graph with non negative edge weights is an np hard problem, for which no known polynomial time algorithm exists. suppose one simply negates each of the edge weights and runs bellman ford to compute shortest paths. Shortest paths and cheapest paths this applet presents the bellman ford algorithm, which calculates shortest paths even when cost can be negative. what do you want to do first? test the algorithm! read a detailed description of the algorithm. Describe how the bellman ford algorithm detects the negative cycles. provide an exam ple graph with negative cycles and show how it can be detected. bellman ford solves the shortest single path issue in which edge weight may be negative, but there is no negative cycle. The bellman ford algorithm is a very popular algorithm used to find the shortest path from one node to all the other nodes in a weighted graph. in this tutorial, we’ll discuss the bellman ford algorithm in depth. Correctness theorem: suppose that g is a weighted graph without negative weight cycles and let s denote the source node. then bellman ford correctly calculates the shortest path distances from s. proof: every shortest path has at most |v| 1 edges. by fact 1 and 2, the distance estimate d[v] is equal to the shortest path length after |v| 1. If g contains no negative cycles reachable from s, the algorithm returns true and d[v] = (s; v) for all v 2 v . if g does contain a negative weight cycle, the algorithm returns false.
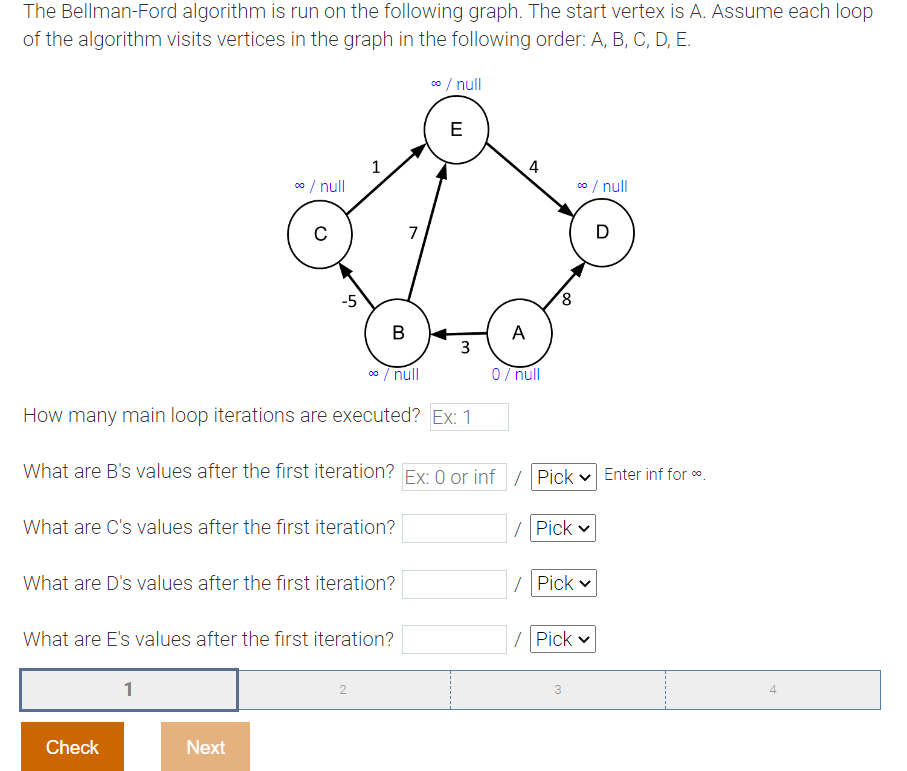
Solved The Bellman Ford Algorithm Is Run On The Following Chegg Describe how the bellman ford algorithm detects the negative cycles. provide an exam ple graph with negative cycles and show how it can be detected. bellman ford solves the shortest single path issue in which edge weight may be negative, but there is no negative cycle. The bellman ford algorithm is a very popular algorithm used to find the shortest path from one node to all the other nodes in a weighted graph. in this tutorial, we’ll discuss the bellman ford algorithm in depth. Correctness theorem: suppose that g is a weighted graph without negative weight cycles and let s denote the source node. then bellman ford correctly calculates the shortest path distances from s. proof: every shortest path has at most |v| 1 edges. by fact 1 and 2, the distance estimate d[v] is equal to the shortest path length after |v| 1. If g contains no negative cycles reachable from s, the algorithm returns true and d[v] = (s; v) for all v 2 v . if g does contain a negative weight cycle, the algorithm returns false.
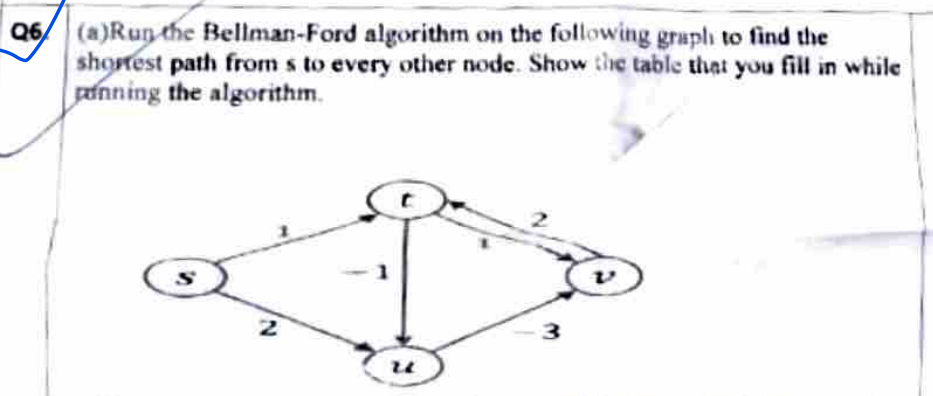
Solved Q6 A Run The Bellman Ford Algorithm On The Chegg Correctness theorem: suppose that g is a weighted graph without negative weight cycles and let s denote the source node. then bellman ford correctly calculates the shortest path distances from s. proof: every shortest path has at most |v| 1 edges. by fact 1 and 2, the distance estimate d[v] is equal to the shortest path length after |v| 1. If g contains no negative cycles reachable from s, the algorithm returns true and d[v] = (s; v) for all v 2 v . if g does contain a negative weight cycle, the algorithm returns false.
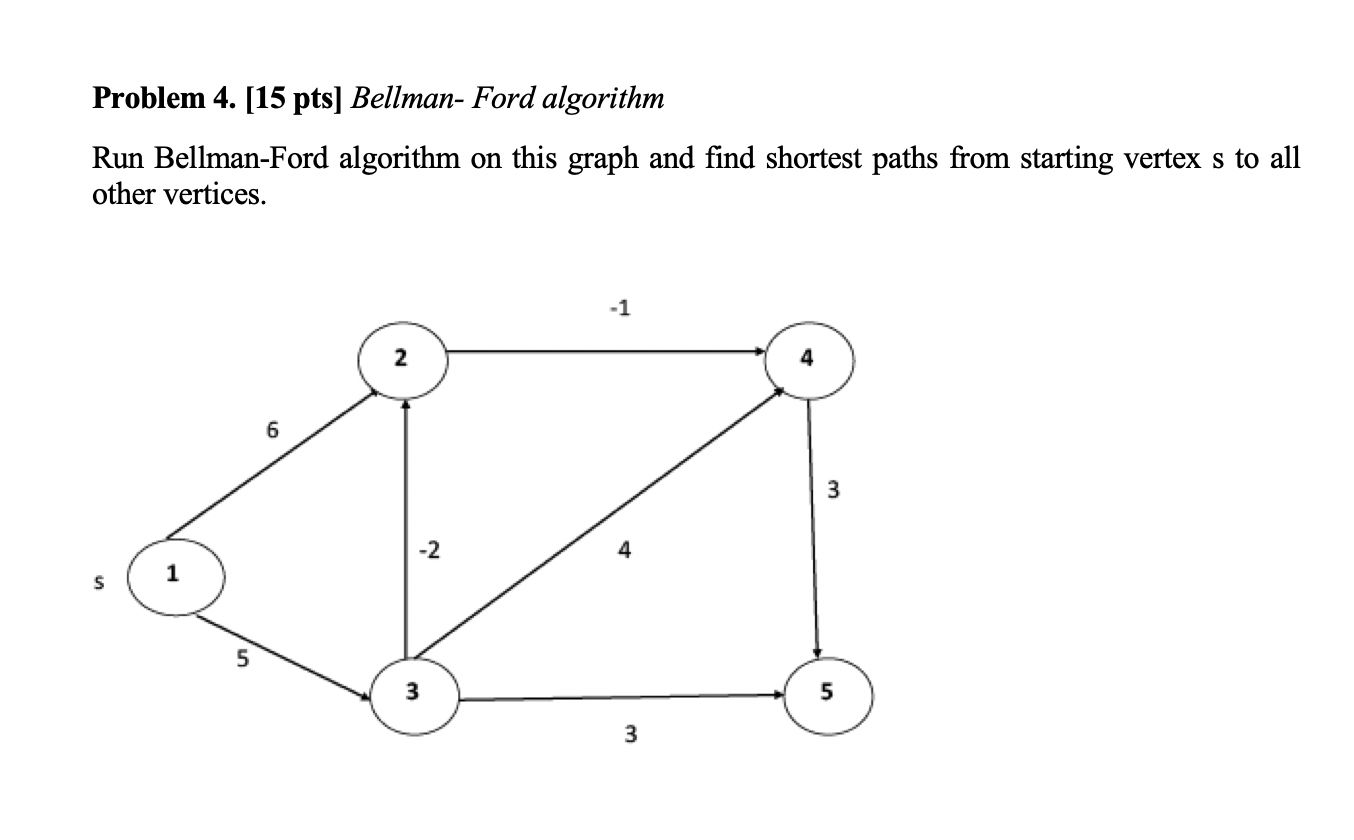
Solved Problem 4 15 Pts Bellman Ford Algorithm Run Chegg
Comments are closed.