Solved Problem 3 Prove That For All N%d1%82%d0%b8%d0%b8n With N%d1%82%d0%b9%d0%b54 We Have Chegg

Solved Problem 2 I Prove That N We shall prove the statement by using the method of mathematical induction. proving for n=1 for n=1, l.h.s= 1 2 = 1 r. h. s = 1 (1 1) (2 × 1 1) 6 = 1 since l.hs=r.h.s:. p (n) is true for n=1. We showed in the induction step that a(n 1) holds, assuming that a(n) holds. in other words, we showed in the induction step that a(n) >a(n 1) holds for all n >= 1. proof. we prove this by induction on n. let a(n) be the assertion of the theorem. induction basis: since 1 = 12, it follows that a(1) holds. induction step: suppose that a(n) holds.

Solved Problem 1 Prove That N 2 3 For All N 4 Chegg 3. verify that for all n the formula solution. for any integer n 1, the sum of the squares of the rst 2n positive integers is given by 12 22 32 n(2n 1)(4n 1). To prove that p (n) is true for all positive integers n, where p (n) is a propositional function we: basis step: we verify that p (1) is true inductive step: we show the conditional statement p (k) → p (k 1) is true for all positive integers k. Consider the statement: for all integers n, if n is even then 8 n is even. (a) prove the statement. what sort of proof are you using? (b) is the converse true? prove or disprove. the statement 'if n is even then 8n is even' is true and proven by direct proof. the converse 'if 8n is even then n is even' is also true and proven by direct proof. A student was asked to prove a statement p (n) by induction. he proved that p (k 1) is true whenever p (k) is true for all k > 5 ∈ n and also that p (5) is true. on the basis of this he could conclude that p (n) is true for all n ∈ n for all n > 5 for all n ≥ 5 for all n < 5.

Solved Problem 3 Prove That For All Nтииn With Nтйе4 We Have Chegg Consider the statement: for all integers n, if n is even then 8 n is even. (a) prove the statement. what sort of proof are you using? (b) is the converse true? prove or disprove. the statement 'if n is even then 8n is even' is true and proven by direct proof. the converse 'if 8n is even then n is even' is also true and proven by direct proof. A student was asked to prove a statement p (n) by induction. he proved that p (k 1) is true whenever p (k) is true for all k > 5 ∈ n and also that p (5) is true. on the basis of this he could conclude that p (n) is true for all n ∈ n for all n > 5 for all n ≥ 5 for all n < 5. Prove by induction: find a, and prove the postulate by mathematical induction. for all n> a, n!> n3 for all n> a, n!> n 3. where ! refers to factorial. so far i've done a bit of it, i'll skip right to the inductive statement and assume that k!>k3 k!> k 3, then try to prove (k 1)!> (k 1)3 (k 1)!> (k 1) 3. Step 1: show it's true for n = 1 1^3 2 (1) = 3, which is divisible by 3 step 2: assume it's true for any integer k then k^3 2k = 3m, where m is an integer. Solution to prove that n! > 3n for all integers n ≥ 7, we can use the method of mathematical induction. base case first, we need to verify the base case, n = 7. 7! = 7 * 6 * 5 *. There are 2 steps to solve this one. you are asked to prove the statement p(n) for all n≥t (for some value of t ) show that 0⋅1 1⋅2 2⋅3 3⋅4 ⋯ (n)(n 1)= 3n(n 1)(n 2) what is the correct base case for this statement? p (t) for which value of t ? 0 1 2 3 p (n) is false for all n. not the question you’re looking for?.

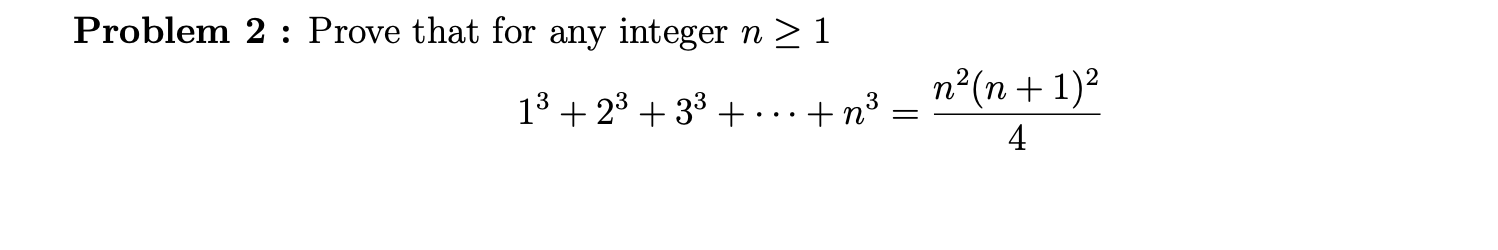
Solved Problem 2 Prove That For Any Integer Nтйе1 Chegg Prove by induction: find a, and prove the postulate by mathematical induction. for all n> a, n!> n3 for all n> a, n!> n 3. where ! refers to factorial. so far i've done a bit of it, i'll skip right to the inductive statement and assume that k!>k3 k!> k 3, then try to prove (k 1)!> (k 1)3 (k 1)!> (k 1) 3. Step 1: show it's true for n = 1 1^3 2 (1) = 3, which is divisible by 3 step 2: assume it's true for any integer k then k^3 2k = 3m, where m is an integer. Solution to prove that n! > 3n for all integers n ≥ 7, we can use the method of mathematical induction. base case first, we need to verify the base case, n = 7. 7! = 7 * 6 * 5 *. There are 2 steps to solve this one. you are asked to prove the statement p(n) for all n≥t (for some value of t ) show that 0⋅1 1⋅2 2⋅3 3⋅4 ⋯ (n)(n 1)= 3n(n 1)(n 2) what is the correct base case for this statement? p (t) for which value of t ? 0 1 2 3 p (n) is false for all n. not the question you’re looking for?. Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on.

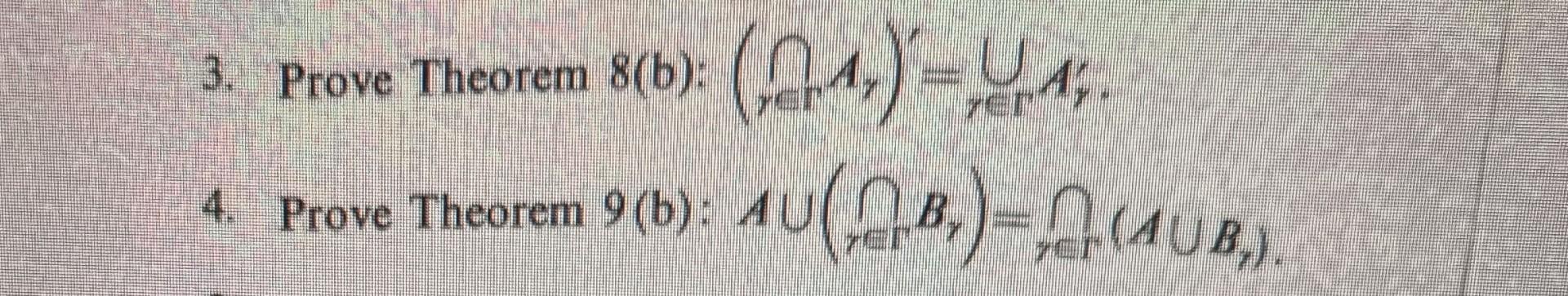
Solved 3 Prove Theorem 8 B Chegg Solution to prove that n! > 3n for all integers n ≥ 7, we can use the method of mathematical induction. base case first, we need to verify the base case, n = 7. 7! = 7 * 6 * 5 *. There are 2 steps to solve this one. you are asked to prove the statement p(n) for all n≥t (for some value of t ) show that 0⋅1 1⋅2 2⋅3 3⋅4 ⋯ (n)(n 1)= 3n(n 1)(n 2) what is the correct base case for this statement? p (t) for which value of t ? 0 1 2 3 p (n) is false for all n. not the question you’re looking for?. Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on.

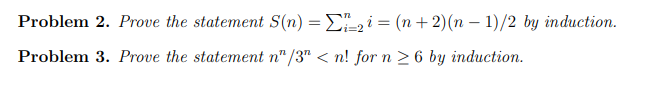
Solved Problem 2 Prove The Statement Chegg Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on.