Solved Problem 2 Prove The Statement Chegg
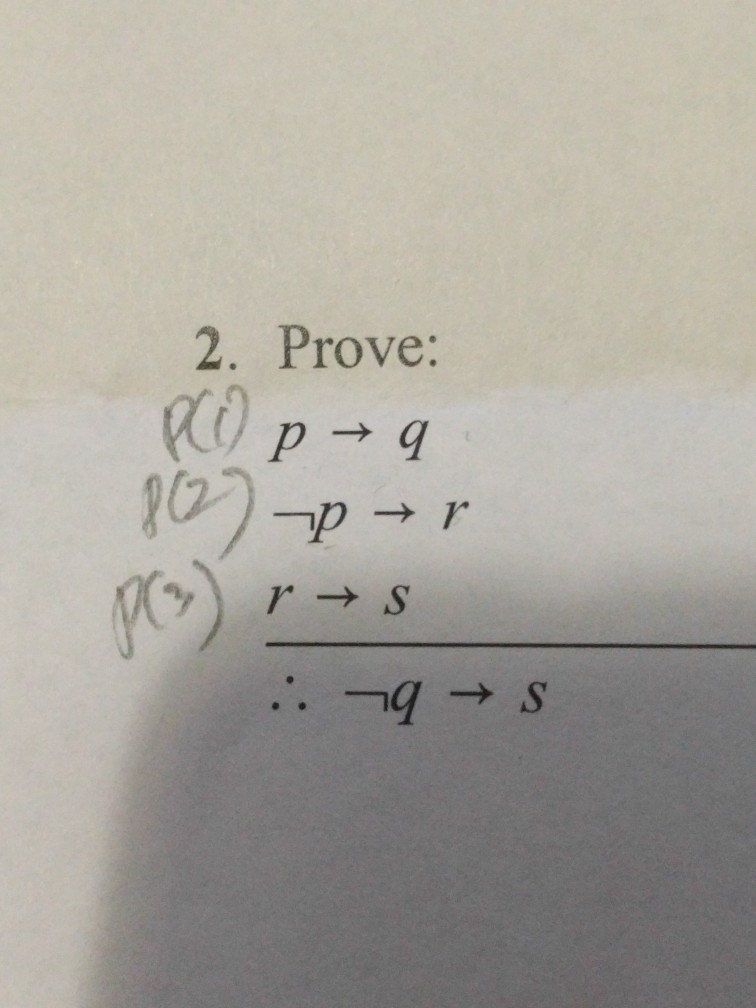
Solved 2 Prove Chegg Step 1 sure, let's prove both of these statements by mathematical induction. problem 1: prove the statement s (n) = ∑ (i = 2 → n) i = (n 2) (n − 1) 2. Several problems with detailed solutions on mathematical induction are presented. let us denote the proposition in question by p (n), where n is a positive integer. the proof involves two steps: step 1: we first establish that the proposition p (n) is true for the lowest possible value of the positive integer n.
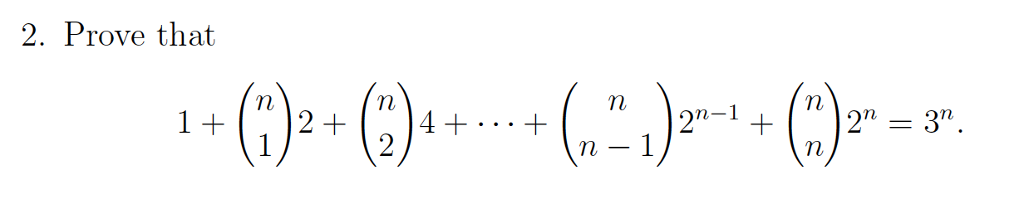
Solved 2 Prove That Chegg Check your proof: propositional first order premises (separate with “,” or “;”): conclusion: create problem. What 2 formulas are used for the proofs calculator? take what is given build a bridge using corollaries, axioms, and theorems to get to the declarative statement. In order to prove a mathematical statement involving integers, we may use the following template: suppose p(n), ∀n ≥ n0, n, n0 ∈ z p (n), ∀ n ≥ n 0, n, n 0 ∈ z be a statement. Problem 2. prove the following statements (a) verify that if q (u)=u⊤v u⊤au, then ∂u∂q=v 2au, where u,v∈rn×1,a∈rn×n is a symmetric matrix, and ∂q ∂u= (∂q ∂u1,…,∂q ∂un)⊤. (b) using part (a) compute ∂β∂q for the least squares objective function for the simple linear regression. what is the name of these equations?.

Solved Prove Chegg In order to prove a mathematical statement involving integers, we may use the following template: suppose p(n), ∀n ≥ n0, n, n0 ∈ z p (n), ∀ n ≥ n 0, n, n 0 ∈ z be a statement. Problem 2. prove the following statements (a) verify that if q (u)=u⊤v u⊤au, then ∂u∂q=v 2au, where u,v∈rn×1,a∈rn×n is a symmetric matrix, and ∂q ∂u= (∂q ∂u1,…,∂q ∂un)⊤. (b) using part (a) compute ∂β∂q for the least squares objective function for the simple linear regression. what is the name of these equations?. Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. see answer. For each of the following statements, translate it into predicate logic and prove it, if the statement is true, or disprove it, otherwise: 1. for any two even integers, there exists a third integer (even or odd) the double of which is equal to the sum of the first two integers. Question: problem 2. prove or disprove the following statements in case you want to prove that they are false, note that for 1, 2 and 3 the negation would start with "there exist sets a,b,c such that ". 1. (1 point) for all sets a,b and c we have a\ (b∪c)= (a\b)∪ (a\c). 2. (1 point) for all sets a,b and c we have if a=b\c, then b=a∪c. 3. Understand the problem: carefully read and understand what you are trying to prove. identify the given information and the statement you need to reach as the conclusion.

Solved Prove Chegg Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. see answer. For each of the following statements, translate it into predicate logic and prove it, if the statement is true, or disprove it, otherwise: 1. for any two even integers, there exists a third integer (even or odd) the double of which is equal to the sum of the first two integers. Question: problem 2. prove or disprove the following statements in case you want to prove that they are false, note that for 1, 2 and 3 the negation would start with "there exist sets a,b,c such that ". 1. (1 point) for all sets a,b and c we have a\ (b∪c)= (a\b)∪ (a\c). 2. (1 point) for all sets a,b and c we have if a=b\c, then b=a∪c. 3. Understand the problem: carefully read and understand what you are trying to prove. identify the given information and the statement you need to reach as the conclusion.

Solved Question 1 And 2 Are Solved By Chegg Experts Please Chegg Question: problem 2. prove or disprove the following statements in case you want to prove that they are false, note that for 1, 2 and 3 the negation would start with "there exist sets a,b,c such that ". 1. (1 point) for all sets a,b and c we have a\ (b∪c)= (a\b)∪ (a\c). 2. (1 point) for all sets a,b and c we have if a=b\c, then b=a∪c. 3. Understand the problem: carefully read and understand what you are trying to prove. identify the given information and the statement you need to reach as the conclusion.
Comments are closed.