Solved Problem 2 Prove That For All N%d1%82%d0%b9%d0%b51 That %d1%82%d0%b8%d1%81k 1nf2k Chegg

Solved Problem 2 I Prove That N We showed in the induction step that a(n 1) holds, assuming that a(n) holds. in other words, we showed in the induction step that a(n) >a(n 1) holds for all n >= 1. proof. we prove this by induction on n. let a(n) be the assertion of the theorem. induction basis: since 1 = 12, it follows that a(1) holds. induction step: suppose that a(n) holds. The principle of mathematical induction is used to prove that a given proposition (formula, equality, inequality…) is true for all positive integer numbers greater than or equal to some integer n. let us denote the proposition in question by p (n), where n is a positive integer. the proof involves two steps:.

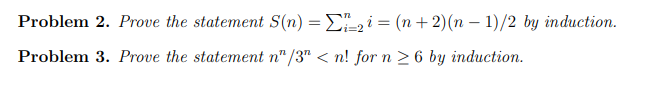
Solved Problem 2 Prove The Statement Chegg Step 1 absolutely, we can prove that the given formula holds true for all n ≥ 2. here's the proof with explanati. To prove that a statement p (n) is true for all integers , n ≥ 0, we use the principle of math induction. the process has two core steps: basis step: prove that p (0) is true. inductive step: assume that p (k) is true for some value of k ≥ 0 and show that p (k 1) is true. video answer. A student was asked to prove a statement p (n) by induction. he proved that p (k 1) is true whenever p (k) is true for all k > 5 ∈ n and also that p (5) is true. on the basis of this he could conclude that p (n) is true for all n ∈ n for all n > 5 for all n ≥ 5 for all n < 5. To prove that p (n) is true for all positive integers n, where p (n) is a propositional function we: basis step: we verify that p (1) is true inductive step: we show the conditional statement p (k) → p (k 1) is true for all positive integers k.

Solved Problem 3 Prove That в ђnв Z Such That Chegg A student was asked to prove a statement p (n) by induction. he proved that p (k 1) is true whenever p (k) is true for all k > 5 ∈ n and also that p (5) is true. on the basis of this he could conclude that p (n) is true for all n ∈ n for all n > 5 for all n ≥ 5 for all n < 5. To prove that p (n) is true for all positive integers n, where p (n) is a propositional function we: basis step: we verify that p (1) is true inductive step: we show the conditional statement p (k) → p (k 1) is true for all positive integers k. For all k ∈n k ∈ n, there exist integers x, y, z x, y, z such that x2 y2 =z2k−1 x 2 y 2 = z 2 k 1. which is even simpler to prove for k = 1 k = 1, while the k → k 1 k → k 1 step is practically identical to the previous statement. Prove that 12 22 ··· n2=1 6 n(n 1)(2n 1) for all n ∈ n. put f(n) = n(n 1)(2n 1) 6. then f(1) = 1, i.e the theorem holds true for n = 1. to prove the theorem, it suffices to assume that it holds true for n = m and derive it for n = m 1, m = 1,2,3, . we have f(m 1)− f(m) = 1 6 (m 1)[(2m 3)(m 2)− m(2m 1)] = 1 6 (m 1)(6m 6) = (m 1)2. We can use induction when we want to show a statement is true for all positive integers n. (note that this is not the only situation in which we can use induction, and that induction is not (usually) the only way to prove a statement for all positive integers.). There are 3 steps to solve this one. this identity can be proven using the binomial theorem. the binomial theorem states that for any rea problem 3. prove that for all positive integers n the following identity holds ∑k=0⌊n 2⌋(n 2k)22k = 23n (−1)n. not the question you’re looking for? post any question and get expert help quickly.