Solved Problem 1 40 Points Order Of Growth This Problem Chegg

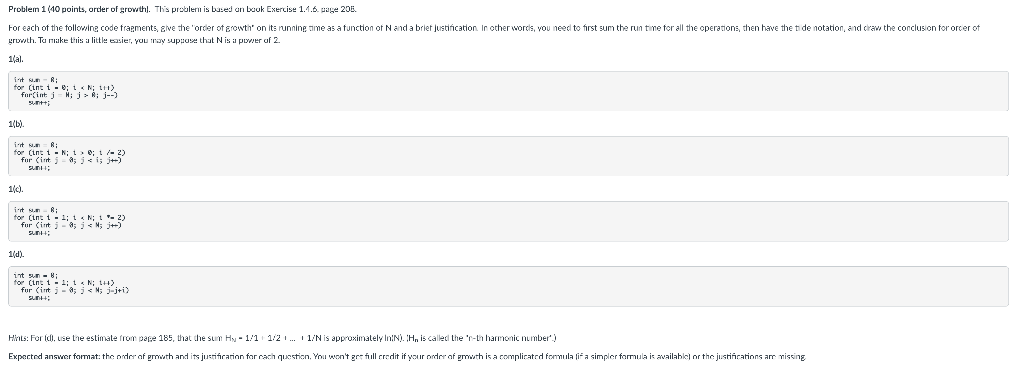
Solved Problem 1 40 Points Order Of Growth This Problem Chegg For each of the following code fragments, give the "order of growth" on its running time as a function of n and a brief justification. in other words, you need to first sum the run time for all the operations, then have the tilde notation, and draw the conclusion. your solution’s ready to go!. Rank the following functions by order of growth; that is, find an arrangement g1, g2, . . . , g30 of the functions satisfying g1 = Ω(g2), g2 = Ω(g3), . . . , g29 = Ω(g30). partition your list into equivalence classes such that f(n) and g(n) are in the same class if and only if f(n) = Θ(g(n)). lg(lg∗ n) lg(n!) n!.

Solved Problem 1 40 Points Order Of Growth This Problern Chegg The order of growth of an algorithm is an approximation of the time required to run a computer program as the input size increases. the order of growth ignores the constant factor needed for fixed operations and focuses instead on the operations that increase proportional to input size. We say that r (n) has order of growth (f (n)), written r (n) = (f (n)) (pronounced "theta of f (n)"), if there are positive constants k1 and k2 independent of n such that for any sufficiently large value of n. (in other words, for large n, the value r (n) is sandwiched between k1f (n) and k2f (n).). Problem 1 1. ranking functions by order of growth the ranking is based on the following facts: exponential functions grow faster than polynomial functions, which grow faster than logarithmic functions; the base of a logarithm does not matter asymptotically, but the base of an exponential and the degree of a polynomial do matter. On the long run each one "wins" against the lower ones (e.g. rule 5 wins over 4,3,2 and 1) (1 3)^n this is bound by a constant! o (1) log (log n) log of a log must grow slower than log of a linear function. n! factorial grows faster than any exponential. how one should prove this?.

Solved 1 Order Of Growth 20 Points Order The Following Chegg Problem 1 1. ranking functions by order of growth the ranking is based on the following facts: exponential functions grow faster than polynomial functions, which grow faster than logarithmic functions; the base of a logarithm does not matter asymptotically, but the base of an exponential and the degree of a polynomial do matter. On the long run each one "wins" against the lower ones (e.g. rule 5 wins over 4,3,2 and 1) (1 3)^n this is bound by a constant! o (1) log (log n) log of a log must grow slower than log of a linear function. n! factorial grows faster than any exponential. how one should prove this?. √ 1. 2.1) order the following functions by growth rate: n, n, n1.5, n2, n log n, n log log n, n log2 n, n log(n2), 2 n, 2n, 2n 2, 37, n2 log n, n3. indicate which functions grow at the same rate. √ solution: 2 n, 37, n, n, n log log n, n log n, n log(n2), n log2 n, n1.5, n2, n2 log n, n3, 2n 2, 2n. n log n and n log(n2) grow at the same rate. There are 5 main orders of growth, each describing how fast a function's runtime grows, as its inputs get bigger. we use the symbol theta to denote an order of growth. constant growth. logarithmic growth. linear growth. quadratic growth. exponential growth. Question: problem 4. (20 points) sort the functions by order of growth from slowest to fastest. state the final ordering and for each pair of adjacent functions in your ordering, explain briefly. note: you have strictly derived some big o bounds in the previous two questions. Problem 1. (4 points) order the following functions by growth rate:𝑁, √𝑁,𝑁1.5,𝑁2 , 𝑁𝑙𝑜𝑔𝑁, 𝑁𝑙𝑜𝑔𝑙𝑜𝑔𝑁, 𝑁𝑙𝑜𝑔2𝑁, 𝑁𝑙𝑜𝑔 (𝑁2), 2 𝑁, 2𝑁, 2𝑁 2, 37,𝑁2log n,𝑁3 . indicate which functions grow at the same rate. problem 2. (6 points) for each of the following six program fragments, give an analysis of the running time (big oh will do).