Solved A Find The Radius Of Convergence Of This Power Chegg There are 2 steps to solve this one. (a) given the power series is ∑ n = 0 ∞ (− 1) n x n 2 n = ∑ n = 0 ∞ a n x n . where a n = (− 1) n 2 n . not the question you’re looking for? post any question and get expert help quickly. If the power series only converges for x =a x = a then the radius of convergence is r = 0 r = 0 and the interval of convergence is x = a x = a. likewise, if the power series converges for every x x the radius of convergence is r = ∞ r = ∞ and interval of convergence is −∞
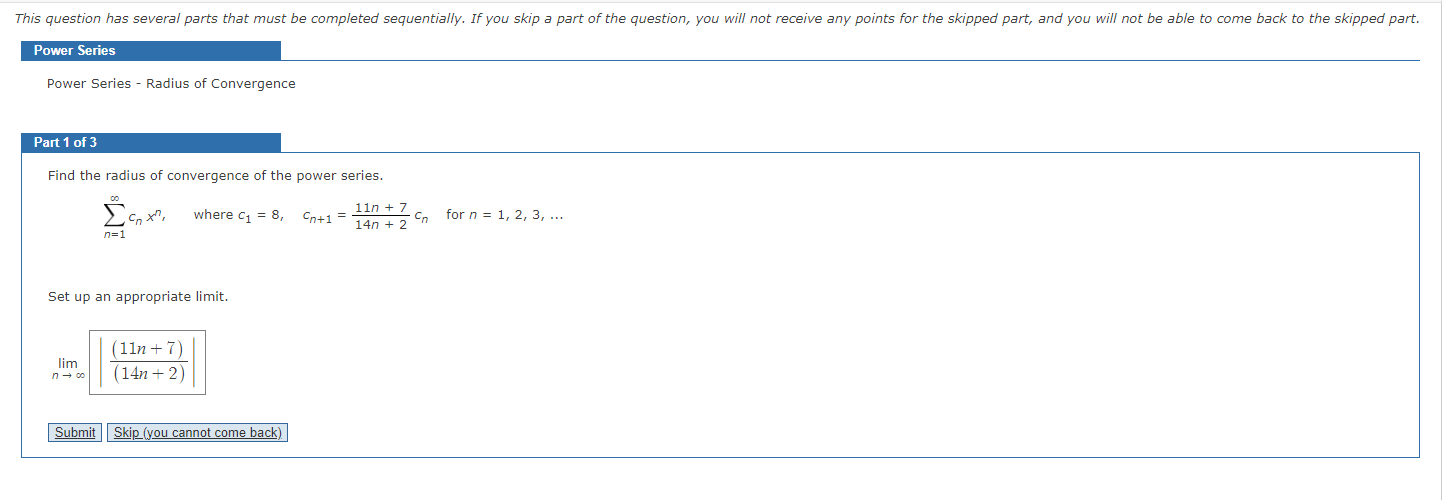
Solved Power Series Power Series Radius Of Convergence Chegg An n!1 jxjn ¢ = jxj 2n 3 and it easily follows that the radius of convergence is r = 1. 2 when it comes to the last series, ̄nally, we have (n 1)! = ¢ ¢ ¢ = an n! n! (2n 2)! xn (2n 1)(2n 2) and this implies that ̄ ̄ ̄ = lim ̄. Find the radius and interval of convergence of these power series. 1. the radius of convergence is 1, the interval of convergence is [ 1,1). 1. apply the ratio test lim n → ∞ | (xn 1 √ (n 1)) (x n √n)| = lim n → ∞ |x|⋅√ (n (n 1)) = |x| by the ratio test, the series converges for |x| < 1, that is, 1 < x < 1. the radius of convergence is 1. One possible choice for the n's are polynomials, which leads to power series solutions. in this section, we seek solutions to linear odes like. the disadvantages of the method are that solutions will be useful only near x0 where the sum converges, and that the solution is an in nite series. Theorem: [fundamental convergence theorem for power series] 1 given a power series p an(x a)n centered at x = a, let r be the n=0 radius of convergence.
Solved Power Series 1 Find The Radius Of Convergence And Chegg One possible choice for the n's are polynomials, which leads to power series solutions. in this section, we seek solutions to linear odes like. the disadvantages of the method are that solutions will be useful only near x0 where the sum converges, and that the solution is an in nite series. Theorem: [fundamental convergence theorem for power series] 1 given a power series p an(x a)n centered at x = a, let r be the n=0 radius of convergence. Using the ratio test, we can find the radius of convergence of given power series as explained below. step 1: let a n = c n (x – a) n and a n 1 = c n 1 (x – a) n 1. step 2: consider the limit for the absolute value of a n 1 a n as n → ∞. i.e., step 3: simplify the ratio. , i.e., (1 cn)cn 1 (x – a) and apply the limit. To find the radius of convergence of a power series, we will use the following two tests: ratio test and root test. by ratio test, the radius of convergence r of a power series a 0 a 1 x a 2 x 2 … = ∑ a n x n is given by. 1 r = lim n→∞ | a n 1 a n |. statement: if r is the radius of convergence of a power series ∑ a n x n, then we have:. Find the radius of convergence and interval of convergence of the series. here’s the best way to solve it. i use defini … problem 2. multiple choice. 1. if the power series f (x 2)" has radius of convergence r=3, then the series (a) convergent (b) divergent (c) inconclusive has radius of 7 ne (n!) 2 (!2 is 2. For each of the following power series determine the interval and radius of convergence. here is a set of practice problems to accompany the power series section of the series & sequences chapter of the notes for paul dawkins calculus ii course at lamar university.
Comments are closed.