Solved Let U Be A Differentiable Function On R2 And Let Chegg

Solved 1 Let R в ґxв ґ Let G Be A Differentiable Function Of Chegg Let u be a differentiable function on r2 and let v(s,t)=u(a(s,t),b(s,t)), where a(s,t)=escost and b(s,t)= essint show that vss(s,t) vtt(s,t)= (a2 b2)(u11(a,b) u22(a,b)) where for simplicity, we wrote a=a(s,t) and b= b(s,t). Let $u=\ { (x,y) \text { in } \mathbb {r}^2 : x 2 y 2 < 4\}$, and let $f (x,y)= \sqrt {4 x 2 y 2}$. prove that $f$ is differentiable, and find its derivative.

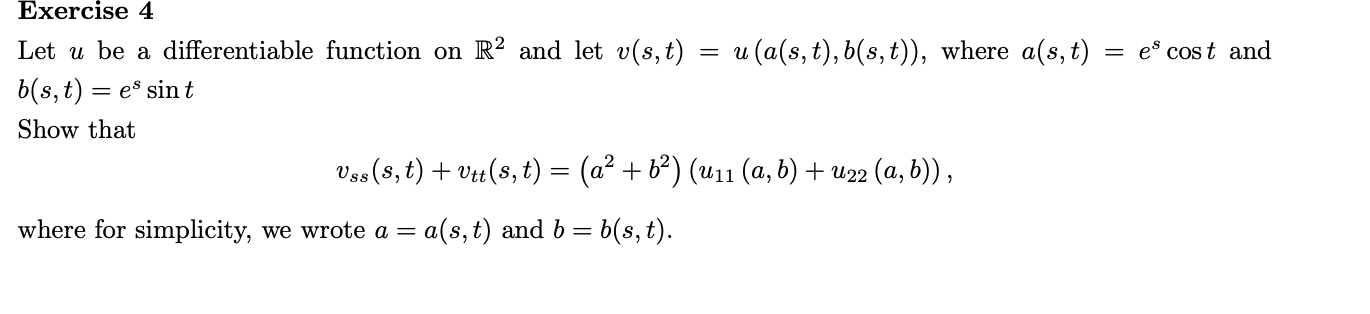
Solved Let U Be A Differentiable Function On R2 And Let Chegg There are 2 steps to solve this one. let g:r3 →r2 be the differentiable function defined by g(u,v,w)=(e−2uv,u2−w2−4u sin(u v w)) and let f:r2 →r2 be the differentiable function f (x,y)=(x2−y,xy). (a) let h(u,v,w)= f ∘g =f (g(u,v,w)). use the chain rule to compute the matrix ∇h(0,0,0). ∇ is the jacobian matrix corresponding to the differential of h. For example, the function f(x) = x2 with derivative f′(x) = 2x is continu ously diferentiable on r, whereas the function in example 8.10 is not continuously diferentiable at 0. Let u : r2r be a continuously differentiable utility function satisfying the usual assumptions, and let f : r$ → r be a monotonic transformation of u. consider the consumer problem of maximizing utility subject to the budget constraint. show that the transformation f = f (u (c)) gives the same solution as u (x). assume an interior solution. ==. ⊂ r c a since there is an open interval (a, b) a with c (a, b). ∈ ⊂ ∈ ior po ivatives. let us give a number of examples that illus trate differentiable and non differentiable mple 4.2. the function f : defined by f(x) = x2 is differe r → r with derivative f′(x) = 2x since r.

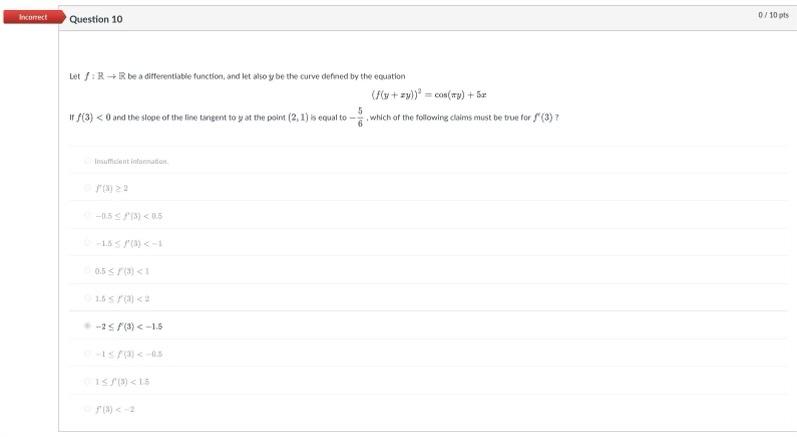
Let F R R Be A Differentiable Function And Let Chegg Let u : r2r be a continuously differentiable utility function satisfying the usual assumptions, and let f : r$ → r be a monotonic transformation of u. consider the consumer problem of maximizing utility subject to the budget constraint. show that the transformation f = f (u (c)) gives the same solution as u (x). assume an interior solution. ==. ⊂ r c a since there is an open interval (a, b) a with c (a, b). ∈ ⊂ ∈ ior po ivatives. let us give a number of examples that illus trate differentiable and non differentiable mple 4.2. the function f : defined by f(x) = x2 is differe r → r with derivative f′(x) = 2x since r. Let f:r2→r be a differentiable function andu (x,y)=f (x y,y x). use the chain rule for partial derivatives to show thatdeludelx deludely=0. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. question: let f:r2→r be a differentiable function andu (x,y)=f (x y,y x). Enter the function you want to find the derivative of in the editor. the derivative calculator supports solving first, second ., fourth derivatives, as well as implicit differentiation and finding the zeros roots. Calculus (a) let f: r2 r be a differentiable function of (x, y), and let (x, y) be the following function of (u, v): a b x= (u) = al c = au (1) с denote by vx the gradient with respect to the (x, y) coordinates, and vu the gradient with respect to the (u, v) coordinates. show that vuf = a vxf. Let w = f (x,y) be a differentiable function with continuous second order partial on r2, where x=auv and y= u−v. show that (i) u∂u∂w −v∂v∂w = (u v)∂y∂w. (ii) if ∂x∂y∂2w = ∂y∂x∂2w, then ∂u∂v∂2w = ∂v∂u∂2w. (iii) ∂u2∂2w ∂v2∂2w =a2(u2 v2) ∂x2∂2w −2αy∂x∂y∂2w 2∂y2∂2w.