Solved If F N N Nlogn G N O N Log N Then It Chegg
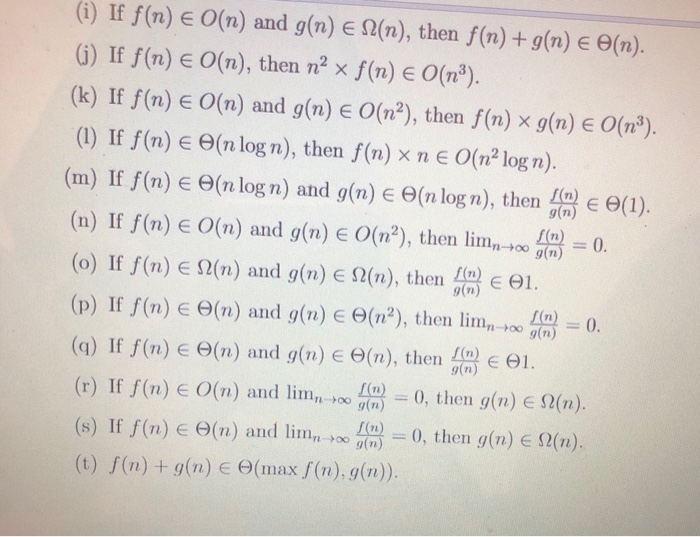
Solved I If F N E 0 N And G N E ω N G If F N E Chegg Here’s the best way to solve it. given f (n) = omega (nlogn) g (n) = Θ (nlo … = = if f (n) = n (nlogn), g (n) = o (n log? n) then it must be the case that f (n) g (n) = (n log? n). == o true o false. not the question you’re looking for? post any question and get expert help quickly. answer to = = if f (n) = n (nlogn), g (n) = o (n log? n) then it. Let f (n) = 2 and g (n) = 1. then f (n) = o (g (n)). however, log (f (n)) = 1 and log (g (n))= 0. there is no n0 nor any c such that 1 <= c * 0. edit: presumably, statement ii is not formatted properly and should read 2^f (n) = o (2^g (n)), which is false if f (n) = 2n and g (n) = n, e.g. see similar questions with these tags.
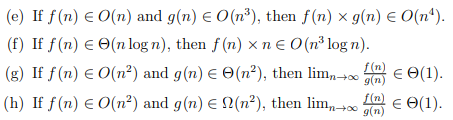
Solved E If F N O N And G N 0 Nº Then F N X Chegg This relation can not be used with the master theorem because f(n) = n log log n f (n) = n log log n does not meet any of the cases. is f(n) = o(n1−ϵ) f (n) = o (n 1 − ϵ)?. F (n) is asymptotically smaller than g (n) if f (n) = o (g (n)). f (n) is asymptotically larger than g (n) if f (n) = ω (g (n)). works. example: t (n) = 2t (n 2) n if n>1, t (n) = 1 if n=1. 1. guess: t (n) = nlog (n) n [because we have exact function instead of asymptotic notation, we will get an exact answer.] 2. There are 2 steps to solve this one. a. prove or disprove 1. if f (n) is o (g (n)). is then 2f (n) = 0 (2 g (n))? 2. f (n) = o (g (n)), then g (n) = o (f (n)). 3. nk = Ø (2") 4. log (n!) = 8 (nlogn) b) in each of the following situations, indicate whether f = o (g), or f = 2 (g), or both f = ølg). 1. 1) arrange the following functions in increasing order of growth rate with g (n) following f (n) in your list if and only if f (n) = o (g (n) 2logn , ( √ 2 )logn , n (logn)3 , 2√2logn , 22 power n , nlogn , 2n power 2 answer: at first we need to convert all pos.
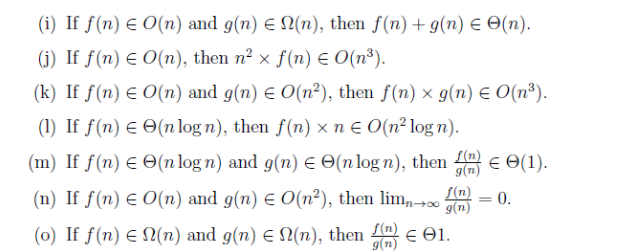
Solved I If F N E O N And G N S N Then F N G N E Chegg There are 2 steps to solve this one. a. prove or disprove 1. if f (n) is o (g (n)). is then 2f (n) = 0 (2 g (n))? 2. f (n) = o (g (n)), then g (n) = o (f (n)). 3. nk = Ø (2") 4. log (n!) = 8 (nlogn) b) in each of the following situations, indicate whether f = o (g), or f = 2 (g), or both f = ølg). 1. 1) arrange the following functions in increasing order of growth rate with g (n) following f (n) in your list if and only if f (n) = o (g (n) 2logn , ( √ 2 )logn , n (logn)3 , 2√2logn , 22 power n , nlogn , 2n power 2 answer: at first we need to convert all pos. We mainly consider the worst case scenario of the algorithm to find its time complexity in terms of big o it’s denoted as o (f (n)), where f (n) is a function that represents the number of operations (steps) that an algorithm performs to solve a problem of size n. To determine if f (n) = o (g (n)), we need to compare the growth rates of f (n) and g (n) as n approach. From the following list of functions compare every unordered pair of functions (all 6). class >, >a , and >p. for each pair show all the operators that are applicable. justify. list: (i) n, (ii) n log n, (iii) n (log n), (iv)n1. b. show that: a 0 a 1 n a 2 n 2 a 3 n 3 aknk= (nk). (20 10) 2. There are 2 steps to solve this one. (i) if f (n)=Θ (n)and g (n)=Ω (n log n)then f (n)= o (g (n)). f(n) = o(n) => f(n) < c1*n for n > n0 and c1 i (i) if f (n)=Θ(n) and g(n)=Ω(nlogn) then f (n)=o(g(n)). (j) if f (n)=Ω(g(n)) and g(n)= Ω(f (n)), then f (n)= Θ(g(n)). not the question you’re looking for? post any question and get expert help quickly.
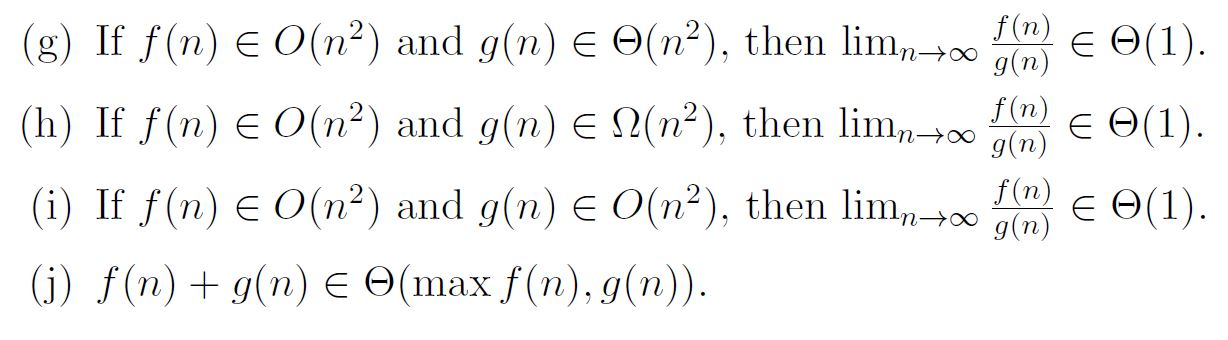
Solved F N G N G If F N E O N And G N E O N Then Chegg We mainly consider the worst case scenario of the algorithm to find its time complexity in terms of big o it’s denoted as o (f (n)), where f (n) is a function that represents the number of operations (steps) that an algorithm performs to solve a problem of size n. To determine if f (n) = o (g (n)), we need to compare the growth rates of f (n) and g (n) as n approach. From the following list of functions compare every unordered pair of functions (all 6). class >, >a , and >p. for each pair show all the operators that are applicable. justify. list: (i) n, (ii) n log n, (iii) n (log n), (iv)n1. b. show that: a 0 a 1 n a 2 n 2 a 3 n 3 aknk= (nk). (20 10) 2. There are 2 steps to solve this one. (i) if f (n)=Θ (n)and g (n)=Ω (n log n)then f (n)= o (g (n)). f(n) = o(n) => f(n) < c1*n for n > n0 and c1 i (i) if f (n)=Θ(n) and g(n)=Ω(nlogn) then f (n)=o(g(n)). (j) if f (n)=Ω(g(n)) and g(n)= Ω(f (n)), then f (n)= Θ(g(n)). not the question you’re looking for? post any question and get expert help quickly.
Comments are closed.