Solved Given The Following Recursive Function Definition Chegg

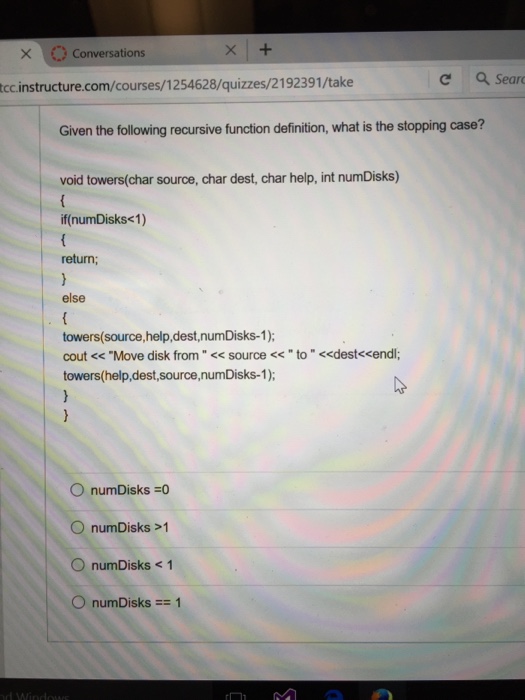
Solved Given The Following Recursive Function Definition Chegg Enhanced with ai, our expert help has broken down your problem into an easy to learn solution you can count on. given the following recursive function definition, what is the stopping case? numdisks = = 1. here’s the best way to solve it. let's analyze each option: 1. **numdisks == 1**: not the question you’re looking for?. In a recursive function, the base case stops the recursion. with recursion, the base case must eventually be reduced to a general case. the following is an example of a recursive function, where nextnum is a function such that nextnum (x) = x 1.

Solved Given The Following Recursive Function Definition Chegg A recursive function (def) is a function which either calls itself or is in a potential cycle of function calls. as the definition specifies, there are two types of recursive functions. consider a function which calls itself: we call this type of recursion immediate recursion. one can view this mathematically in a directed call graph. The process in which a function calls itself directly or indirectly is called recursion and the corresponding function is called a recursive function. a recursive algorithm takes one step toward solution and then recursively call itself to further move. This problem has been solved! you'll get a detailed solution from a subject matter expert that helps you learn core concepts. We say that f is a recursively defined function (or recursive function for short) when it contains a call to itself in its body. we use the term recursive call to describe this inner f(n 1) call. and finally, we use the term recursion to describe the programming technique of defining recursive functions to perform computations and solve problems.

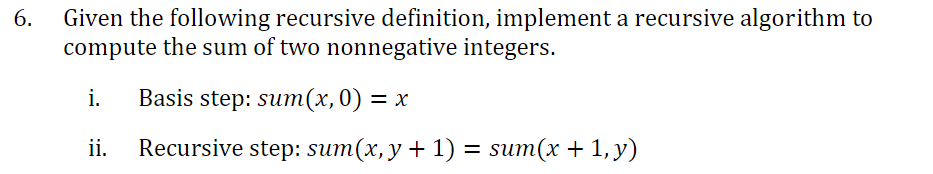
Solved Given The Following Recursive Definition Implement A Chegg This problem has been solved! you'll get a detailed solution from a subject matter expert that helps you learn core concepts. We say that f is a recursively defined function (or recursive function for short) when it contains a call to itself in its body. we use the term recursive call to describe this inner f(n 1) call. and finally, we use the term recursion to describe the programming technique of defining recursive functions to perform computations and solve problems. Determine whether each of these proposed definitions is a valid recursive definition of a function f from the set of nonnegative integers to the set of integers. if f is well defined, find a formula for f (n) when n is a nonnegative integer and prove that your formula is valid. f (0) = 0, f (n) = 2f (n 2) for n ≥ 1 choose the correct statement. To solve, either: top down: record subproblem solutions in a memo and re use (recursion memoization) bottom up: solve subproblems in topological sort order (usually via loops) for fibonacci, n 1 subproblems (vertices) and < 2n dependencies (edges) time to compute is then o(n) additions # recursive solution (top down). Int recursivefun1(int n) { if (n <= 0) return 1; else return 1 recursivefun1(n 1); } this function is being called recursively n times before reaching the base case so its o(n), often called linear. What is the definition of recursion? briefly describe the general steps of recursive problem solving and explain the importance of "base case" and "recursive steps" in recursion.2.  given the following recursive function to calculate triangle numbers:```javapublic static int triangle (int n) {if (n == 1) return 1;return n triangle (n.

Solved Problem 3 Given The Following Recursive Function Chegg Determine whether each of these proposed definitions is a valid recursive definition of a function f from the set of nonnegative integers to the set of integers. if f is well defined, find a formula for f (n) when n is a nonnegative integer and prove that your formula is valid. f (0) = 0, f (n) = 2f (n 2) for n ≥ 1 choose the correct statement. To solve, either: top down: record subproblem solutions in a memo and re use (recursion memoization) bottom up: solve subproblems in topological sort order (usually via loops) for fibonacci, n 1 subproblems (vertices) and < 2n dependencies (edges) time to compute is then o(n) additions # recursive solution (top down). Int recursivefun1(int n) { if (n <= 0) return 1; else return 1 recursivefun1(n 1); } this function is being called recursively n times before reaching the base case so its o(n), often called linear. What is the definition of recursion? briefly describe the general steps of recursive problem solving and explain the importance of "base case" and "recursive steps" in recursion.2.  given the following recursive function to calculate triangle numbers:```javapublic static int triangle (int n) {if (n == 1) return 1;return n triangle (n.