Solved Find The Limit Of The Sequence 1 N N 1 Chegg

Solved 1 Find The Limit Of The Sequence 1 N Oc N N 1 Chegg Question: find the limit of the sequence {a n} n=1^infinity, where an = ( 1)^n ln (n) n. include working to justify the method you use. (b) determine whether the series sigma n=0^infinity n (1 3)^n converges or diverges. (c) (i) for the function f (x) = e^x e^ x, find the taylor polynomials of degree 4 about the centre c = 0. How to find the limit of a sequence, examples and step by step solutions, a series of free online calculus lectures in videos.

Solved Find Find The Limit Of The Sequence Chegg Step 1 the given sequence is {(1 1 3 n) n} n = 1 ∞ now we want to find the limit of the given sequence . Question: use the appropriate limit laws and theorems to determine the limit of the sequence.a (n)=5 ( (1) (7))^ (n) (use symbolic notation and fractions where needed. We haven't proven that 'e' is irrational or that lim (1 (x n))n) =ex (1 (x n)) n) = e x. we only have the properties of sequences like monotone convergence theorem and basic properties to prove this. Definition 3.1 the number l is the limit of the sequence {an} if (1) given ǫ > 0, an ≈ǫ l for n ≫ 1. if such an l exists, we say converges, or is convergent; if not, diverges, or is divergent. {an} {an} the two notations for the limit of a sequence are: n→∞{an} lim = l ; an → l as n → ∞ .
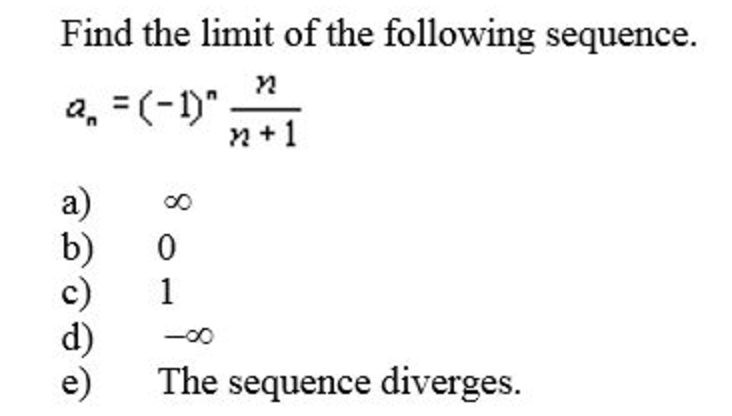
Solved Find The Limit Of The Following Sequence A N Chegg We haven't proven that 'e' is irrational or that lim (1 (x n))n) =ex (1 (x n)) n) = e x. we only have the properties of sequences like monotone convergence theorem and basic properties to prove this. Definition 3.1 the number l is the limit of the sequence {an} if (1) given ǫ > 0, an ≈ǫ l for n ≫ 1. if such an l exists, we say converges, or is convergent; if not, diverges, or is divergent. {an} {an} the two notations for the limit of a sequence are: n→∞{an} lim = l ; an → l as n → ∞ . Given a sequence {an} {a n}, if the terms an a n become arbitrarily close to a finite number l l as n n becomes sufficiently large, we say {an} {a n} is a convergent sequence and l l is the limit of the sequence. in this case, we write. if a sequence {an} {a n} is not convergent, we say it is a divergent sequence. The limit of a sequence is the value the sequence approaches as the number of terms goes to infinity. not every sequence has this behavior: those that do are called convergent, while those that don't are called divergent. limits capture the long term behavior of a sequence and are thus very useful in bounding them. We have already seen that there is a sequence in a set s that converges to inf s and another that converges to sup s: in this section, we investigate other characteristics of sets and points that would guarantee the existence of a sequence of elements within the set that converge to the point. This sequence is represented by list {1, 1, 1, 1, 1, 1, …} {−1,1,−1,1,−1,1,…}. if we take ϵ = 0. 0 1 ϵ = 0.01 then we can't find n n such that for n> n n> n members will be close to some number (limit), because members oscillate: sequence takes by turn values 1 or 1.

Solved 13 Find The Limit Of Each Of The Following Sequence Chegg Given a sequence {an} {a n}, if the terms an a n become arbitrarily close to a finite number l l as n n becomes sufficiently large, we say {an} {a n} is a convergent sequence and l l is the limit of the sequence. in this case, we write. if a sequence {an} {a n} is not convergent, we say it is a divergent sequence. The limit of a sequence is the value the sequence approaches as the number of terms goes to infinity. not every sequence has this behavior: those that do are called convergent, while those that don't are called divergent. limits capture the long term behavior of a sequence and are thus very useful in bounding them. We have already seen that there is a sequence in a set s that converges to inf s and another that converges to sup s: in this section, we investigate other characteristics of sets and points that would guarantee the existence of a sequence of elements within the set that converge to the point. This sequence is represented by list {1, 1, 1, 1, 1, 1, …} {−1,1,−1,1,−1,1,…}. if we take ϵ = 0. 0 1 ϵ = 0.01 then we can't find n n such that for n> n n> n members will be close to some number (limit), because members oscillate: sequence takes by turn values 1 or 1.
Comments are closed.