Solved Design And Analysis Of Algorithms Chegg

Design And Analysis Of Algorithms Pdf Algorithms Theoretical Enhanced with ai, our expert help has broken down your problem into an easy to learn solution you can count on. here’s the best way to solve it. i can help explain concepts or solve specific prob not the question you’re looking for? post any question and get expert help quickly. Our resource for introduction to the design and analysis of algorithms includes answers to chapter exercises, as well as detailed information to walk you through the process step by step.

Solved Design And Analysis Of Algorithms Chegg This is cmsc 451: design and analysis of algorithms. we will cover graphs, greedy algorithms, divide and conquer algorithms, dynamic programming, network ows, np completeness, and approximation algorithms. What is an algorithm? [m – 13] an algorithm is a sequence of unambiguous instructions for solving a problem, i., for obtaining a required output for any legitimate input in finite amount of time. an algorithm is step by step procedure to solve a problem. what are the types of algorithm efficiencies?. Et p (x) = x3 x 1 will design an algorithm to solve the polynomial multiplication problem. in particular, the input to the problem for input size n ≥ 1 are the co ef icients of the two polynomials p0, . . . , pn−1 and q0, . . . , qn−1. the output should be the coefficient r0, . . , r2n−2, where p (x) = pn−1 pi ixi, q(x) = pn. An algorithm is a sequence of unambiguous instructions for solving a computational problem, i.e., for obtaining a required output for any legitimate input in a finite amount of time.

Solved Design And Analysis Of Algorithms Chegg Et p (x) = x3 x 1 will design an algorithm to solve the polynomial multiplication problem. in particular, the input to the problem for input size n ≥ 1 are the co ef icients of the two polynomials p0, . . . , pn−1 and q0, . . . , qn−1. the output should be the coefficient r0, . . , r2n−2, where p (x) = pn−1 pi ixi, q(x) = pn. An algorithm is a sequence of unambiguous instructions for solving a computational problem, i.e., for obtaining a required output for any legitimate input in a finite amount of time. It discusses analyzing algorithms for tasks like adding matrices, matrix multiplication, sorting lists, and solving systems of linear equations. for each algorithm, it considers the basic operations, how many times they are performed based on input size, and whether the operation count can vary for the same input size. Explore the essential concepts of design and analysis of algorithms, including algorithm complexity, types of algorithms, and practical applications. Empirical analysis of algorithms use the experimental approach of algorithmic analysis to compute running time and produce a performance profile of the following sorting techniques: selection sort • insertion sort • merge sort quick sort theoretical background: please refer to section 2.6 empirical analysis of algorithms of your text book. Divide the problem into a number of sub problems that are smaller instances of the same problem. conquer the sub problems by solving them recursively. if the subproblem sizes are small enough, however, just solve the subproblems in a straightforward manner. combine the solutions for the sub problems into the solution for the original problem.

Solved Design And Analysis Of Algorithms Chegg It discusses analyzing algorithms for tasks like adding matrices, matrix multiplication, sorting lists, and solving systems of linear equations. for each algorithm, it considers the basic operations, how many times they are performed based on input size, and whether the operation count can vary for the same input size. Explore the essential concepts of design and analysis of algorithms, including algorithm complexity, types of algorithms, and practical applications. Empirical analysis of algorithms use the experimental approach of algorithmic analysis to compute running time and produce a performance profile of the following sorting techniques: selection sort • insertion sort • merge sort quick sort theoretical background: please refer to section 2.6 empirical analysis of algorithms of your text book. Divide the problem into a number of sub problems that are smaller instances of the same problem. conquer the sub problems by solving them recursively. if the subproblem sizes are small enough, however, just solve the subproblems in a straightforward manner. combine the solutions for the sub problems into the solution for the original problem.
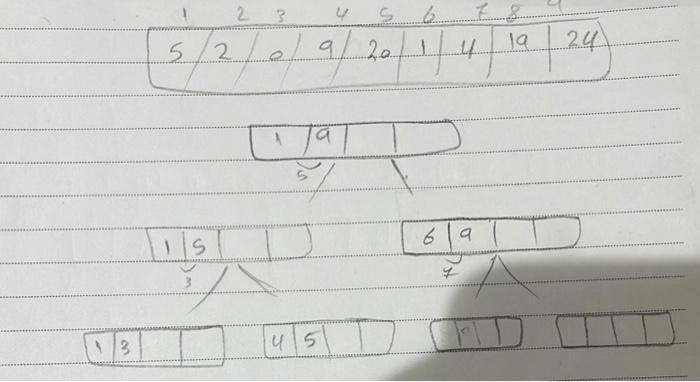
Solved Design And Analysis Of Algorithms Chegg Empirical analysis of algorithms use the experimental approach of algorithmic analysis to compute running time and produce a performance profile of the following sorting techniques: selection sort • insertion sort • merge sort quick sort theoretical background: please refer to section 2.6 empirical analysis of algorithms of your text book. Divide the problem into a number of sub problems that are smaller instances of the same problem. conquer the sub problems by solving them recursively. if the subproblem sizes are small enough, however, just solve the subproblems in a straightforward manner. combine the solutions for the sub problems into the solution for the original problem.

Solved Analysis Of Algorithms Chegg
Comments are closed.