Solved Consider The Sequence Bn 1 Defined Recursively By Chegg

Consider The Sequence Bn Defined Recursively By B1 Chegg There are 2 steps to solve this one. consider the sequence {bn}1 defined recursively by bı = 3 and, for any integer n > 2, bn non 1 find b2, 63, 64, and b5. b2 = 3 b3 3 > b4 = 3 b5 = 3. not the question you’re looking for? post any question and get expert help quickly. Consider the recursively defined sequence {xn} {x n} where xo =c x o = c and xn 1 =axn x n 1 = a x n. show that this sequence can be described by the closed formula xn =can x n = c a n for all n ≥0 n ≥ 0.

Solved Consider The Sequence Bn 1 Defined Recursively By Chegg Consider the sequence defined recursively by (any positive number), and , for which of the following values of must ? repeatedly applying the function, and simplifying, we get and then again. so must appear at every third term after . the only option given of the form is . Consider the sequence \ {b n\} {n=1}^\infty defined recursively by $b 1 = 4$ and, for any integer $n \ge 2$, $b n = nb {n 1}$. find $b 2$, $b 3$, $b 4$, and $b 5$. b 2 = b 3 = b 4 = b 5 = added by timothy w. Concepts recurrence relations, linear homogeneous recurrence, generating functions, infinite series, geometric progression, summation techniques explanation we are given a sequence defined recursively: b1 = 2 b2 = 3 bn 2 = 3bn 1 −bn (n≥ 1) we are asked to compute s = ∑n=1∞ 5nbn. we'll use generating functions and the properties of recurrence relations to solve this sum efficiently. Consider the recursively defined sequence: b0 = 1 b 0 = 1, b1 = 0 b 1 = 0, b2 = 1 b 2 = 1, and for every n ≥ 3 n ≥ 3, bn = bn−1 − 2bn−3 b n = b n 1 2 b n 3.

Solved Consider The Sequence Bn 1 Defined Recursively By Chegg Concepts recurrence relations, linear homogeneous recurrence, generating functions, infinite series, geometric progression, summation techniques explanation we are given a sequence defined recursively: b1 = 2 b2 = 3 bn 2 = 3bn 1 −bn (n≥ 1) we are asked to compute s = ∑n=1∞ 5nbn. we'll use generating functions and the properties of recurrence relations to solve this sum efficiently. Consider the recursively defined sequence: b0 = 1 b 0 = 1, b1 = 0 b 1 = 0, b2 = 1 b 2 = 1, and for every n ≥ 3 n ≥ 3, bn = bn−1 − 2bn−3 b n = b n 1 2 b n 3. Consider the sequence of numbers 𝑏⃗defined recursively as follows: • base case: 𝑏0 = 3. • recursive case: for 𝑛 ⩾ 1, we have 𝑏𝑛 = 2𝑏𝑛−1 𝑛. give a proof by induction that 𝑏𝑛 = 5 × 2𝑛 − 𝑛 − 2 for each natural number 𝑛. consider q (n) to be the statement b n = 5 × 2 n n 2, n ≥ 1. substitute n=1 into the q (n). q (1): b 1 = 5 × 2 1 1 2 = 7. When we define a first order sequence fang recursively, we express anc1 in terms of an and specify a value for a1. we can then compute successive values of an, which might allow us to guess the limit if it exists. Question: consider the sequence {bn}"=1 defined recursively by bı = 3 and, for any integer n >2, bn = nbn 1 find b2, 63, 64, and b5. b2 b3 = 64 b5 show transcribed image text. We will use strong mathematical induction to prove that bn≤3n−1 for all n≥1. base cases: for n=1,2,3, we have b1=1≤31−1=1,b2=3≤32−1=3, and b3=7≤33−1=9, so the inequality holds for the base cases. inductive hypothesis: assume that bk≤3k−1 for all k=1,2, ,n (not just for the base cases).

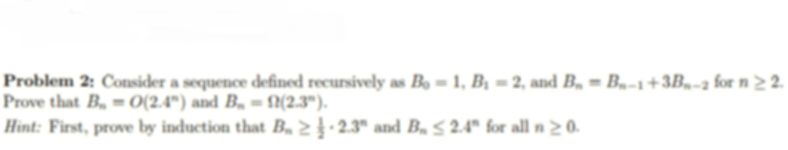
Solved Consider A Sequence Defined Recursively As B0 1 B1 Chegg Consider the sequence of numbers 𝑏⃗defined recursively as follows: • base case: 𝑏0 = 3. • recursive case: for 𝑛 ⩾ 1, we have 𝑏𝑛 = 2𝑏𝑛−1 𝑛. give a proof by induction that 𝑏𝑛 = 5 × 2𝑛 − 𝑛 − 2 for each natural number 𝑛. consider q (n) to be the statement b n = 5 × 2 n n 2, n ≥ 1. substitute n=1 into the q (n). q (1): b 1 = 5 × 2 1 1 2 = 7. When we define a first order sequence fang recursively, we express anc1 in terms of an and specify a value for a1. we can then compute successive values of an, which might allow us to guess the limit if it exists. Question: consider the sequence {bn}"=1 defined recursively by bı = 3 and, for any integer n >2, bn = nbn 1 find b2, 63, 64, and b5. b2 b3 = 64 b5 show transcribed image text. We will use strong mathematical induction to prove that bn≤3n−1 for all n≥1. base cases: for n=1,2,3, we have b1=1≤31−1=1,b2=3≤32−1=3, and b3=7≤33−1=9, so the inequality holds for the base cases. inductive hypothesis: assume that bk≤3k−1 for all k=1,2, ,n (not just for the base cases).