Solved Consider The Following Series %d0%b2 N 1%d0%b2 %d1%9bn31 Evaluate The Chegg

Solved Consider The Following Series 1 N 2 In N Chegg Step 1 the geometric series Σ n = 1 ∞ 2 π n is given. the objective is to determine the common ratio and determine whether. In each of problems 1 through 8, determine the radius of convergence of the given power series. apply the ratio test to determine the condition in which the provided series converges.

Solved Consider The Following Series в ћ N Chegg To check whether the given expression converges or not we will apply ration test and p test. ratio test: let a n is the given expression. let l = lim n ↦ ∞ | a n 1 a n |. if l<1, then the series converges. if l>1, then the series diverges. if l<1, then the test is inconclusive. p series test:. This calculator will try to find the infinite sum of arithmetic, geometric, power, and binomial series, as well as the partial sum, with steps shown (if possible). For each of the following power series, find the interval of convergence and the radius of convergence: notice that an 1 = (−1)n 1(n 1)2xn 1. then lim n→∞. 1)2|x|n 1 = lim n2|x|n n→∞ |x| 2n 2 2 = |x| lim = n→∞ 2n |x| lim = |x|, so this series converges absolutely for n→∞ 2 −1 < x < 1. (−1)nn2 which diverges by the nth term test. Find the sum of the series for those values of x. write the formula in terms of x. not sure how to complete part b. thank you so much! still looking for help? get the right answer, fast. get a free answer to a quick problem. most questions answered within 4 hours. choose an expert and meet online.

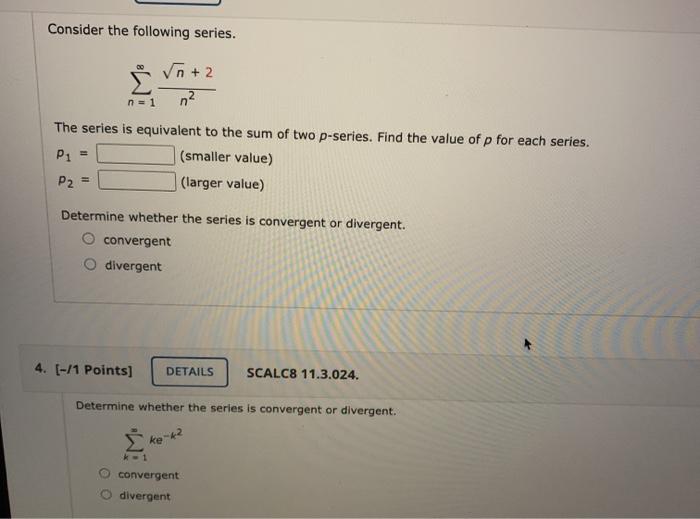
Solved Consider The Following Series Do N 2 N2 N 1 The Chegg For each of the following power series, find the interval of convergence and the radius of convergence: notice that an 1 = (−1)n 1(n 1)2xn 1. then lim n→∞. 1)2|x|n 1 = lim n2|x|n n→∞ |x| 2n 2 2 = |x| lim = n→∞ 2n |x| lim = |x|, so this series converges absolutely for n→∞ 2 −1 < x < 1. (−1)nn2 which diverges by the nth term test. Find the sum of the series for those values of x. write the formula in terms of x. not sure how to complete part b. thank you so much! still looking for help? get the right answer, fast. get a free answer to a quick problem. most questions answered within 4 hours. choose an expert and meet online. Free online series convergence calculator check convergence of infinite series step by step. O the series diverges by the limit comparison test with a divergent geometric series. o the series converges by the limit comparison test with a convergent p series. There are 2 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly. Each term is less than that of a divergent geometric series. determine whether the given alternating series is absolutely convergent, conditionally convergent, or divergent.

Solved Consider The Following Series 00 1 N 2 In N Chegg Free online series convergence calculator check convergence of infinite series step by step. O the series diverges by the limit comparison test with a divergent geometric series. o the series converges by the limit comparison test with a convergent p series. There are 2 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly. Each term is less than that of a divergent geometric series. determine whether the given alternating series is absolutely convergent, conditionally convergent, or divergent. Question: consider the following series: ( 1)" n series a: ΣΙ series b: Σε ( 1)" series c: ln=1 ( 1)" (n 1) vn2 1 select all of the statements that are true about these series.