Solved Consider The Following Function F Chegg

Solved 1 Consider The Following Function 1 Consider The Chegg There are 4 steps to solve this one. it is given that the function is f (x) = x 1 x. the objective is to find graph and max and min values. the concept. Free functions calculator explore function domain, range, intercepts, extreme points and asymptotes step by step.

Solved Consider The Following Function Chegg To find (g∘f)^ ( 1), we first need to determine (g∘f) and then find its inverse. (g∘f) (x) = g (f (x)) = g (x 5) = 4 (x 5) 7 = 4x 20 7 = 4x 13. to find the inverse, we interchange x and y in the function (g∘f) (x) = 4x 13 and solve for y. x = 4y 13. rearranging the equation to solve for y: 4y = x 13, y = (x 13) 4. Free math problem solver answers your calculus homework questions with step by step explanations. Solutions for homework section 6.4 and 6.5 problem 1: for each of the following functions do the following: (i) write the function as piecewise function and sketch its graph, (ii) write the function as a combination of terms of the form ua(t)k(t a) and compute the laplace transform. For the following exercises, use the function f represented in table 14 below. evaluate f (3). solve f (x) = 1 more.

Solved Question 4 Consider The Following Function F T Chegg Solutions for homework section 6.4 and 6.5 problem 1: for each of the following functions do the following: (i) write the function as piecewise function and sketch its graph, (ii) write the function as a combination of terms of the form ua(t)k(t a) and compute the laplace transform. For the following exercises, use the function f represented in table 14 below. evaluate f (3). solve f (x) = 1 more. To integrate \ ( f (x) \) from − 1 to 4, we need to split the integral into two parts because the function. For example, consider the piecewise function: f (x) = {2 x 1 x ≤ 0 3 x x> 0 this function uses the expression 2x 1 when x is less than or equal to 0, and 3x when x is greater than 0. (iii) use rouche's theorem to prove that a polynomial of degree n has n roots in c. solution: (i) by the argument principle, the change in argument of f(z) as z travels around the circle is equal to (2 ) the number of zeros minus poles of f(z) inside the circle, so just the number of zeros then. Suppose a function f(t) has fourier transform f (ω) = 2πjωe−|ω|. is f(t) purely real? is f(t) purely imaginary? is f(t) even? is f(t) odd? what is f(0)? calculate f(t) and verify these properties. hint: for finding the inverse fourier transform, use this property: let g(w) = 2πe^(−|ω|) and f(ω) = jωg(ω) and use the derivative property.

Solved Problem 2 Consider The Following Function F X Chegg To integrate \ ( f (x) \) from − 1 to 4, we need to split the integral into two parts because the function. For example, consider the piecewise function: f (x) = {2 x 1 x ≤ 0 3 x x> 0 this function uses the expression 2x 1 when x is less than or equal to 0, and 3x when x is greater than 0. (iii) use rouche's theorem to prove that a polynomial of degree n has n roots in c. solution: (i) by the argument principle, the change in argument of f(z) as z travels around the circle is equal to (2 ) the number of zeros minus poles of f(z) inside the circle, so just the number of zeros then. Suppose a function f(t) has fourier transform f (ω) = 2πjωe−|ω|. is f(t) purely real? is f(t) purely imaginary? is f(t) even? is f(t) odd? what is f(0)? calculate f(t) and verify these properties. hint: for finding the inverse fourier transform, use this property: let g(w) = 2πe^(−|ω|) and f(ω) = jωg(ω) and use the derivative property.
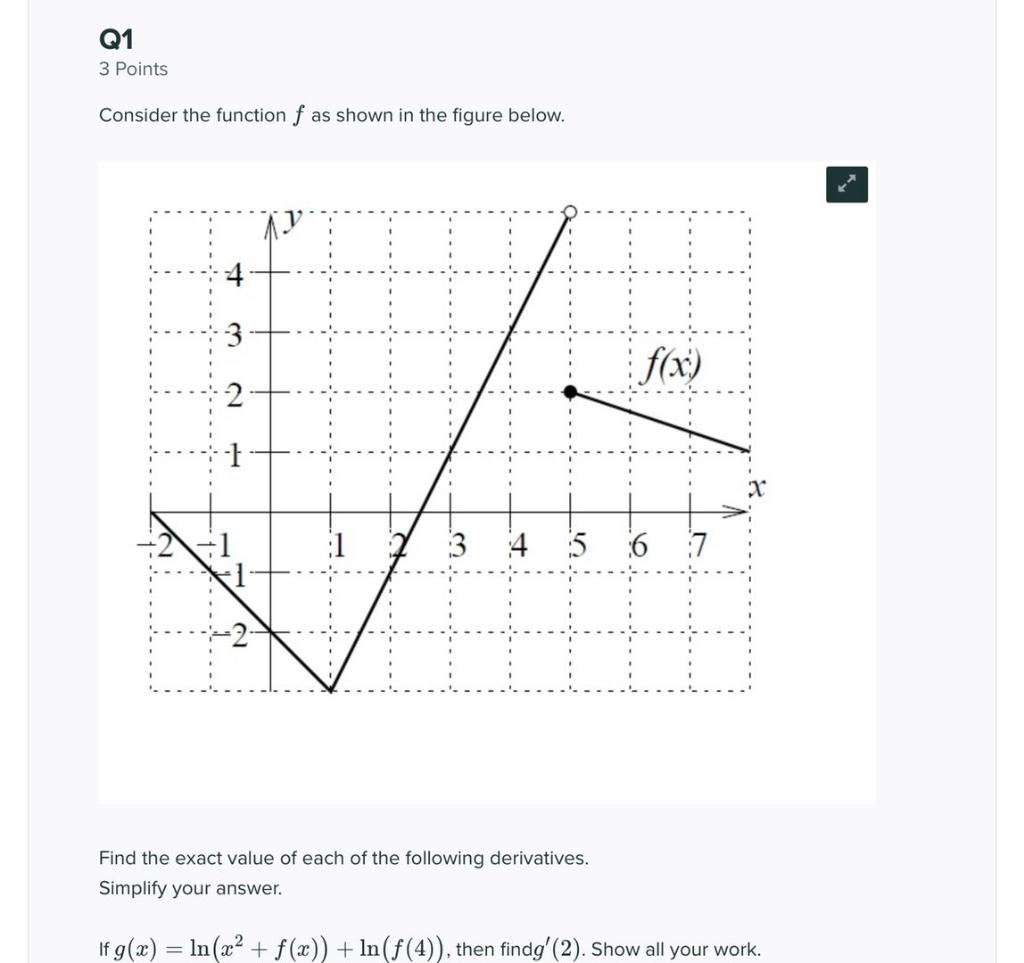
Solved Consider The Function F As Shown In The Figure Below Chegg (iii) use rouche's theorem to prove that a polynomial of degree n has n roots in c. solution: (i) by the argument principle, the change in argument of f(z) as z travels around the circle is equal to (2 ) the number of zeros minus poles of f(z) inside the circle, so just the number of zeros then. Suppose a function f(t) has fourier transform f (ω) = 2πjωe−|ω|. is f(t) purely real? is f(t) purely imaginary? is f(t) even? is f(t) odd? what is f(0)? calculate f(t) and verify these properties. hint: for finding the inverse fourier transform, use this property: let g(w) = 2πe^(−|ω|) and f(ω) = jωg(ω) and use the derivative property.
Comments are closed.