Solved 10 Use The Graphical Method For Linear Programming To Chegg

Solved Problem 2 Linear Programming Graphical Methoda Chegg Use the graphical method for linear programming to find the optimal solution for the following problem. maximize p = 4x 5 y subject to 2x 4y ≤ 12 5x 2y ≤ 10 and x ≥ 0, y ≥ 0. graph the feasible region. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. The graphical method for solving linear programming problems is a powerful visualization tool for problems with two variables. by plotting constraints and identifying the feasible region, one can find the optimal solution by evaluating the objective function at the corner points.

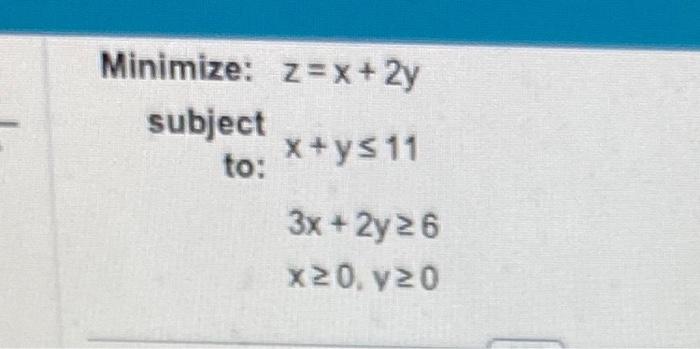
Solved 7 2 Linear Programming The Graphical Methoduse Chegg Graphical method calculator solve the linear programming problem using graphical method, step by step online. Solving linear programming problems using the graphical method example designing a diet a dietitian wants to design a breakfast menu for certain hospital patients. the menu is to include two items a and b. suppose that each ounce of. The graphical method is a visual technique used to solve linear programming problems that involve two decision variables. it works by plotting the linear inequality constraints on a graph to identify a feasible region. This document discusses linear programming and provides an example problem to demonstrate how to solve a linear programming problem using the graphical method. it begins by defining linear programming and its objective of maximizing or minimizing quantities under linear constraints.

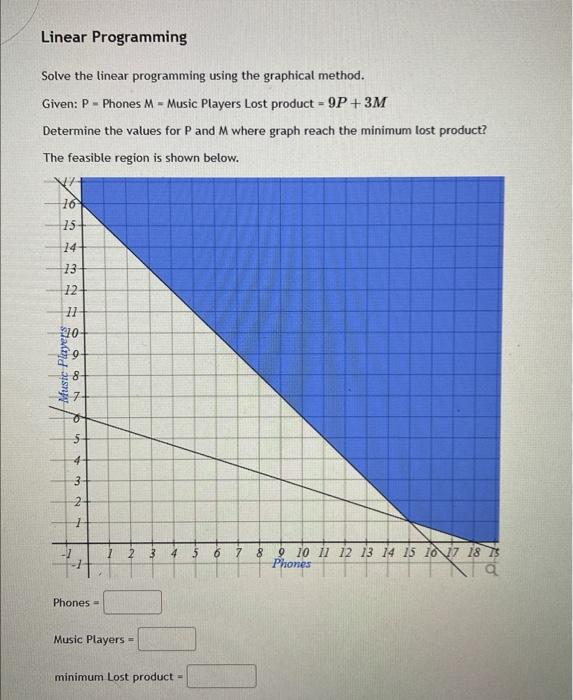
Solved Linear Programming Solve The Linear Programming Using Chegg The graphical method is a visual technique used to solve linear programming problems that involve two decision variables. it works by plotting the linear inequality constraints on a graph to identify a feasible region. This document discusses linear programming and provides an example problem to demonstrate how to solve a linear programming problem using the graphical method. it begins by defining linear programming and its objective of maximizing or minimizing quantities under linear constraints. The graphical solution method, or geometric method, allows for solving simple lp problems intuitively and visually. this method is exclusively used when there are two or three decision variables, as it is impossible to illustrate more than 3 dimensions graphically. Solve the following linear programming model by using the graphical method: graph the constraints and identify the feasible region. using the corner points method, determine the optimal solution (s) (show your work). To find the optimal solutions at which the maximum and minimum occur, we substitute each corner point into the objective function, p = 10 x − 3 y . we now look at our chart for the highest function value (the maximum) and the lowest function value (the minimum). the maximum value is 32 and it occurs at the point ( 5, 6 ) . State the decision variables, formulate the objective function and the constraints. tabulate data if needed. 2. graph the constraints in quadrant i where the decision variables serve as the axes. lp problems are restricted by the nonnegativity constraint. 3.

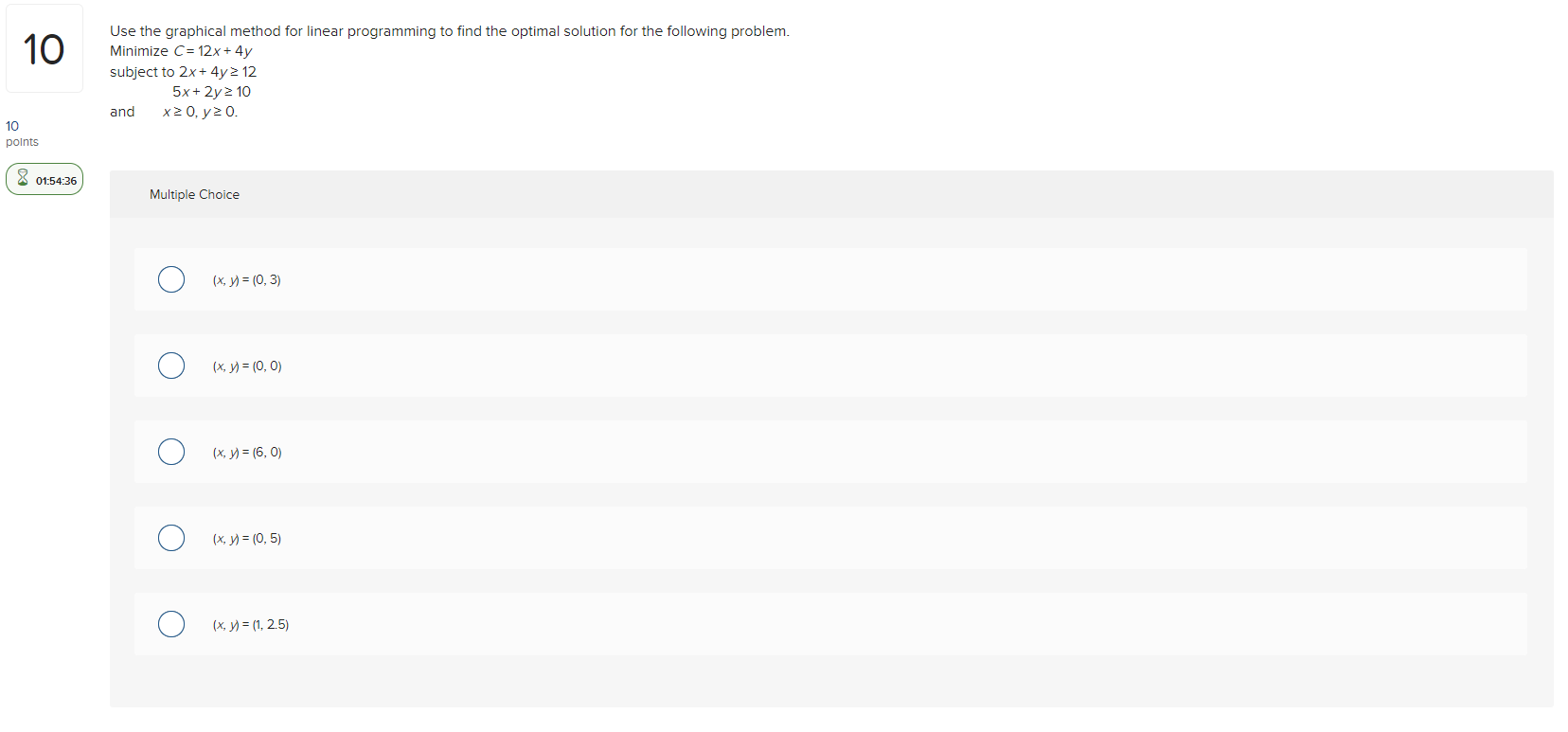
Solved 10 Use The Graphical Method For Linear Programming To Chegg The graphical solution method, or geometric method, allows for solving simple lp problems intuitively and visually. this method is exclusively used when there are two or three decision variables, as it is impossible to illustrate more than 3 dimensions graphically. Solve the following linear programming model by using the graphical method: graph the constraints and identify the feasible region. using the corner points method, determine the optimal solution (s) (show your work). To find the optimal solutions at which the maximum and minimum occur, we substitute each corner point into the objective function, p = 10 x − 3 y . we now look at our chart for the highest function value (the maximum) and the lowest function value (the minimum). the maximum value is 32 and it occurs at the point ( 5, 6 ) . State the decision variables, formulate the objective function and the constraints. tabulate data if needed. 2. graph the constraints in quadrant i where the decision variables serve as the axes. lp problems are restricted by the nonnegativity constraint. 3.