Solved 1 Vector Spaces Examples Determine If The Following Chegg

Solved 1 Vector Spaces Examples Determine If The Following Chegg Vector spans determine whether the vectors in the set s span the vector space v given. assume the field is real numbers and that vector addition and scalar. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. question: 1. Show that the set of all real polynomials with a degree n ≤ 3 associated with the addition of polynomials and the multiplication of polynomials by a scalar form a vector space.

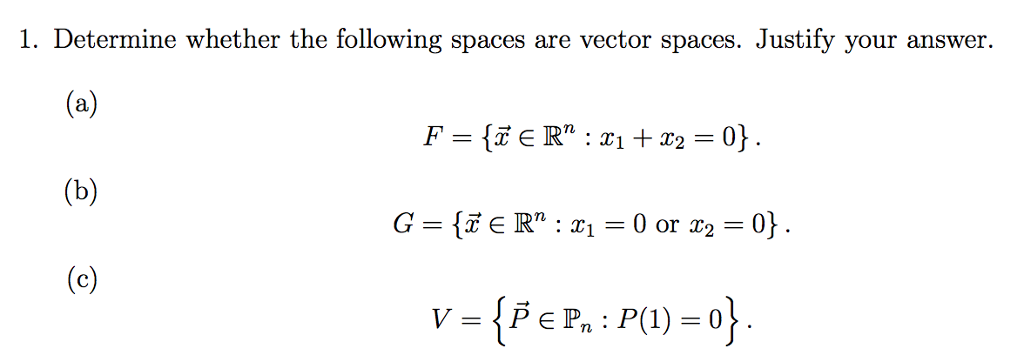
Solved 1 Determine Whether The Following Spaces Are Vector Chegg Determine which of the following sets is a vector space. $v$ is the line $y=x$, in the $xy$ plane: $v =\ { [x,y]: \; y=x\}$ $w$ is the union of the first and second quadrants in the $xy$ plane: $w=. It is easy to check that k is a vector space over f since the required axioms are just a subset of the statements that are valid for the eld k . we thus obtain many examples this way:. Vector spaces may be formed from subsets of other vectors spaces. these are called subspaces. for each u and v are in h, u v is in h. (in this case we say h is closed under vector addition.) for each u in h and each scalar c, cu is in h. (in this case we say h is closed under scalar multiplication.). The vector space r2 is represented by the usual xy plane. each vector v in r2 has two components. the word “space” asks us to think of all those vectors—the whole plane. each vector gives the x and y coordinates of a point in the plane: similarly the vectors in r3 correspond to points .x; y; z v d .x; y . in three dimensional space.

Solved Problems 1 2 Determine Which Of The Following Chegg Vector spaces may be formed from subsets of other vectors spaces. these are called subspaces. for each u and v are in h, u v is in h. (in this case we say h is closed under vector addition.) for each u in h and each scalar c, cu is in h. (in this case we say h is closed under scalar multiplication.). The vector space r2 is represented by the usual xy plane. each vector v in r2 has two components. the word “space” asks us to think of all those vectors—the whole plane. each vector gives the x and y coordinates of a point in the plane: similarly the vectors in r3 correspond to points .x; y; z v d .x; y . in three dimensional space. Definition 4.3.1 a nonempty subset w of a vector space v is called a subspace of v if w is a vector space under the operations addition and scalar multiplication defined in v. Determine whether or not the following examples are real vector spaces. if so, make sure to show why each of the 10 vector space axioms hold. if not, give a counter example showing that at least one axiom fails. (a) (4 points) the set of all (1,2) € r2 with the operations of addition (@) and scalar multiplication (%) defined by: (:11,12) (91.92) =. In the study of 3 space, the symbol (a1, a2, a3) has two different geometric in terpretations: it can be interpreted as a point, in which case a1, a2 and a3 are the coordinates, or it can be interpreted as a vector, in which case a1, a2 and a3 are the components. For each of the following sets, determine if it is a vector space over r. if it is, give an explicit basis and compute its dimension. if it isn't, explain why not by giving an example of how one of the vector space properties fails. (a) the set of points in r3 with x 0. (b) the set of points in r2 with y. (c) the set of points in r3 with r y.