Solved 1 Point Consider The Sequence Recursively Defined Chegg
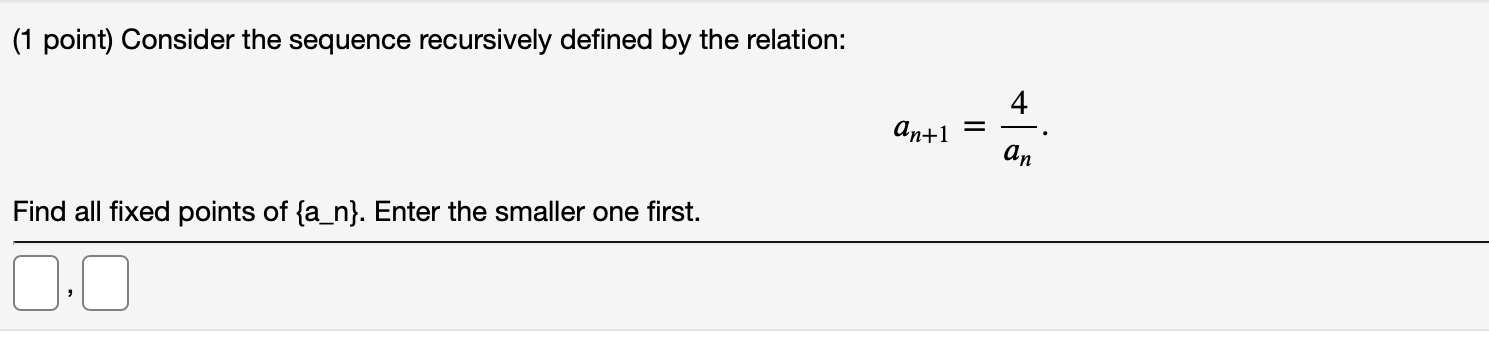
Solved 1 Point Consider The Sequence Recursively Defined Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. there are 4 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly. (a) (2 3x)2 solution: expand the polynomial to see that it is 4 12x 9x2, so the corresponding sequence with this generating function is 4, 12, 9, 0, 0, 0, : : :.

Solved Consider The Following Sequence Defined Recursively Chegg Recursive sequences often cause students a lot of confusion. before going into depth about the steps to solve recursive sequences, let's do a step by step examination of 2 example problems. Every time you were asked in school to look at a sequence of numbers, find a pattern, and give the next number in the sequence, you were probably working out a recurrence relation and applying it. consider the sequence 5, 8, 11, 14. what number should come next? solution. We want to be able to show the relationship between the recursive definition and the explicit definition for a sequence. in this section we will look at proving an explicit sequence satisfies a given recurrence relation. There is yet another way to describe a sequence. this process is known as recursion. recursion is the process of choosing a starting term and repeatedly applying the same process to each term to arrive at the following term. recursion requires that you know the value of the term or terms immediately before the term you are trying to find.
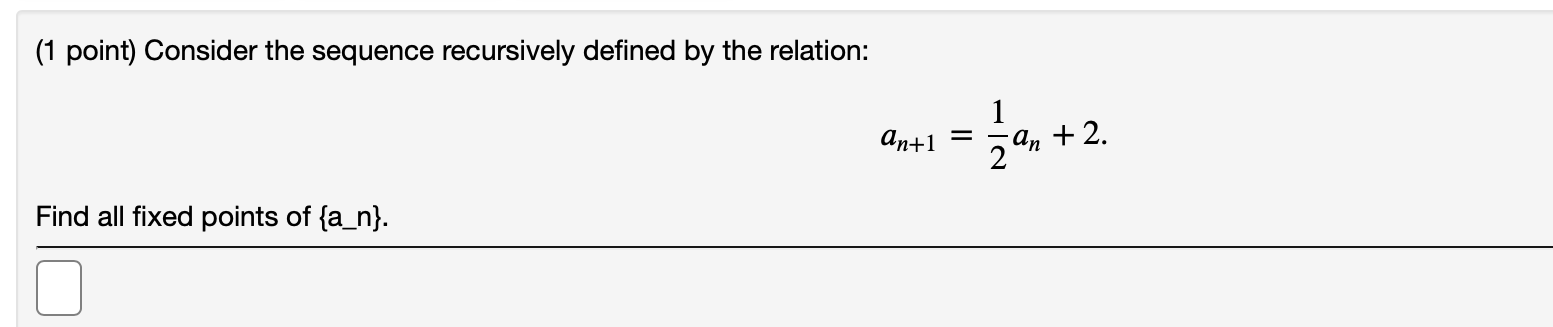
Solved 1 Point Consider The Sequence Recursively Defined Chegg We want to be able to show the relationship between the recursive definition and the explicit definition for a sequence. in this section we will look at proving an explicit sequence satisfies a given recurrence relation. There is yet another way to describe a sequence. this process is known as recursion. recursion is the process of choosing a starting term and repeatedly applying the same process to each term to arrive at the following term. recursion requires that you know the value of the term or terms immediately before the term you are trying to find. Lucky for us, there are a few techniques for converting recursive definitions to closed formulas. doing so is called solving a recurrence relation. recall that the recurrence relation is a recursive definition without the initial conditions. for example, the recurrence relation for the fibonacci sequence is f n = f n−1 f n−2. Question: recursive definitions of sequence $a n = n (n 1)$ and $a n = n^2$. my attempt: for the first one,$a n = n (n 1)$, i first manually generate a sequence using $n \geq 1$, $$2, 6, 12, 20, 3. Question: consider the sequence 4,7,10,13,16, with a1=4 a) give a recursive definition for the sequence. select the variable names from the vars box to use in your definition. an= b) give a closed formula for the nth term of the sequence. an= c) is 2017 a term in the sequence? ? no yes d) how many terms does the. Using the recursive formula, we have: a3 = a2 a1 = 1 1 = 2 a4 = a3 a2 = 2 1 = 3 so, a4 = 3. now, let's assume that a4n is divisible by 3 for some integer n ≥ 1. we want to prove that a4 (n 1) is also divisible by 3.

Solved 1 Point Consider The Sequence Defined Recursively Chegg Lucky for us, there are a few techniques for converting recursive definitions to closed formulas. doing so is called solving a recurrence relation. recall that the recurrence relation is a recursive definition without the initial conditions. for example, the recurrence relation for the fibonacci sequence is f n = f n−1 f n−2. Question: recursive definitions of sequence $a n = n (n 1)$ and $a n = n^2$. my attempt: for the first one,$a n = n (n 1)$, i first manually generate a sequence using $n \geq 1$, $$2, 6, 12, 20, 3. Question: consider the sequence 4,7,10,13,16, with a1=4 a) give a recursive definition for the sequence. select the variable names from the vars box to use in your definition. an= b) give a closed formula for the nth term of the sequence. an= c) is 2017 a term in the sequence? ? no yes d) how many terms does the. Using the recursive formula, we have: a3 = a2 a1 = 1 1 = 2 a4 = a3 a2 = 2 1 = 3 so, a4 = 3. now, let's assume that a4n is divisible by 3 for some integer n ≥ 1. we want to prove that a4 (n 1) is also divisible by 3.
Comments are closed.