Solved 1 Given The Digits 1 2 5 6 And 9 How Many Chegg

Given The Digits 1 1 2 3 5 5 6 7 How Many Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. question: 1. given the digits 1,2,5,6, and 9. how many 3 digit numbers can be formed from these digits if no two digits are to be the same? of the numbers formed in (a) how many are even? how many are odd? how many are greater than 600 ?. To solve the problem with the digits 1, 2, 5, 6, and 9, we will analyze each part step by step. a. total 3 digit numbers with unique digits. to form a 3 digit number using these digits where no two digits are the same, we can use the permutation formula. we have: so, the total number of 3 digit numbers can be calculated as: 5×4×3=60.

Solved 1 Given The Digits 1 2 5 6 And 9 How Many Chegg Solution: we have 4 choices for the first letter, 3 choices for the second letter, 2 choices for the third letter and 1 choice for the fourth letter. hence the number of words is given by 4 × 3 × 2 × 1 = 4! = 24. example 3: how many 2 digit numbers can you make using the digits 1, 2, 3 and 4 without repeating the digits?. Question 1192086: given the digits 1,2,4,6,8 and 9, how many four digit numbers can be formed if repetition is not allowed. you can put this solution on your website! any of remaining 3 digits in the last position, giving 3 options. 6*5*4*3 = 360 different numbers. solved. in this site. Explanation 1 identify the even digits that can be used for the ones place. the even digits are 2, 6 2 since repetitions are not allowed, there are 4 choices for the first digit, 3 choices for the second digit, and 2 choices for the third digit 3 calculate the total number of combinations: 4 \times 3 \times 2 = 24 4×3× 2=24. 1. given the digits 1, 2, 5, 6, and 9. a. how many 3 digit numbers can be formed from these digits if no two digits are to be the same? b. of the numbers formed in (a) how many are even? how many are odd? how many are greater than 600? c. how many numbers can be formed if digit may be repeated?.

Question Chegg Explanation 1 identify the even digits that can be used for the ones place. the even digits are 2, 6 2 since repetitions are not allowed, there are 4 choices for the first digit, 3 choices for the second digit, and 2 choices for the third digit 3 calculate the total number of combinations: 4 \times 3 \times 2 = 24 4×3× 2=24. 1. given the digits 1, 2, 5, 6, and 9. a. how many 3 digit numbers can be formed from these digits if no two digits are to be the same? b. of the numbers formed in (a) how many are even? how many are odd? how many are greater than 600? c. how many numbers can be formed if digit may be repeated?. To form a 3 digit number, we have 5 choices for the first digit (1, 2, 5, 6, or 9), 4 choices for the second digit (since we can't repeat the first digit), and 3 choices for the third digit (since we can't repeat any of the previous digits). Question: given the digits 1, 2, 5, 6, and 9. a. how many 3 digit numbers can be formed from these digits if no two digits are to be the same? b. of the numbers formed in (a) how many are even? how many are odd? how many are greater than 600? c. how many numbers can be formed if digit may be repeated? given the digits 1, 2, 5, 6, and 9. a. This allows us to use the digits 1, 5, and 9 to fill in the remaining places, leading to a total of 6 unique combinations. the final answer is 6 possible numbers. Consider the digits 1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 ,9 part a: repetition of numbers is not allowed 1) how many numbers consist of two distinct digits could be formed out of the given digits ?.
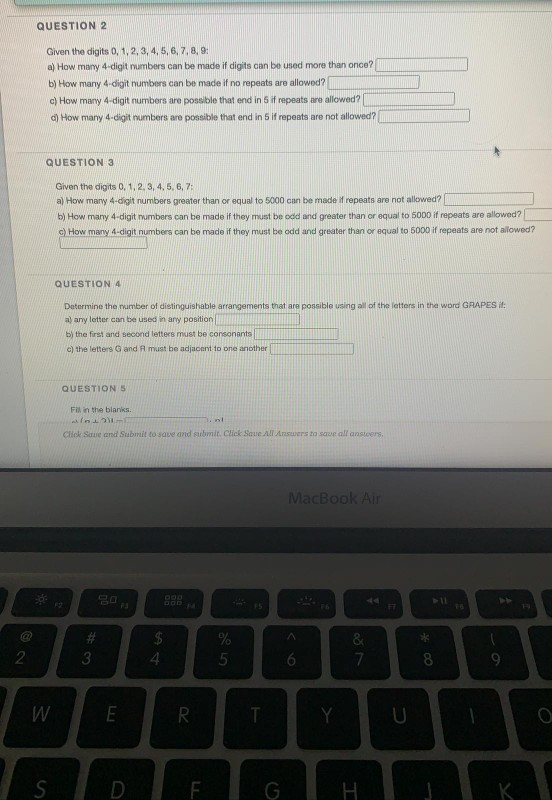
Solved Question 2 Given The Digits 0 1 2 3 4 5 6 7 8 9 A Chegg To form a 3 digit number, we have 5 choices for the first digit (1, 2, 5, 6, or 9), 4 choices for the second digit (since we can't repeat the first digit), and 3 choices for the third digit (since we can't repeat any of the previous digits). Question: given the digits 1, 2, 5, 6, and 9. a. how many 3 digit numbers can be formed from these digits if no two digits are to be the same? b. of the numbers formed in (a) how many are even? how many are odd? how many are greater than 600? c. how many numbers can be formed if digit may be repeated? given the digits 1, 2, 5, 6, and 9. a. This allows us to use the digits 1, 5, and 9 to fill in the remaining places, leading to a total of 6 unique combinations. the final answer is 6 possible numbers. Consider the digits 1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 ,9 part a: repetition of numbers is not allowed 1) how many numbers consist of two distinct digits could be formed out of the given digits ?.
Comments are closed.