Quicksort Algorithm Interviewbit
Github Jalalsayed1 Quicksort Algorithm Variant Implementations Of Algorithm quicksort(a, lo, hi) is if lo < hi then p := partition(a, lo, hi) quicksort(a, lo, p) quicksort(a, p 1, hi) hoare partition scheme vs lomuto partition scheme the pivot selection the execution speed of the algorithm depends largely on how this mechanism is implemented, poor implementation can assume that the algorithm is run at a. Quicksort has less overhead, so with small n and slow computers, it is better. but computers are so fast today that the additional overhead of a mergesort is negligible, and the risk of a very slow quicksort far outweighs the insignificant overhead of a mergesort in most cases.

Algorithm 12 Quicksort How can i write a stable implementation of the quicksort algorithm in javascript?. I am trying to find out how (using a quicksort algorithm) to sort an struct array by 2 criterias. for example say i had a struct of: struct employee{ char gender[12]; char name[12]; int i. I have been working on one of my programs related to the implementation of quick sort. the code below is a quick sort algorithm that selects the median of three elements as the pivot. but the thin. The space complexity of quicksort is listed as o(logn). however quicksort can process without use of any additional memory: at each iteration, during the partition process, the entries are sw.
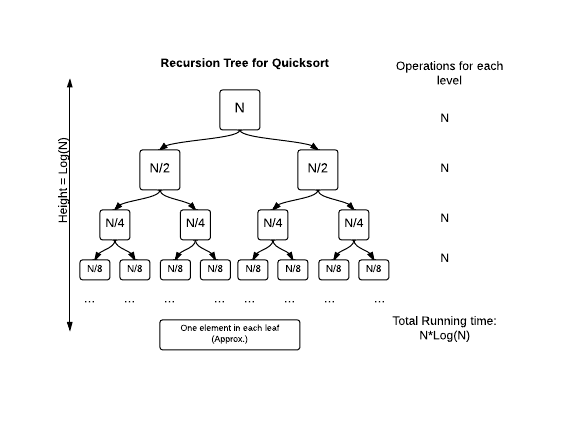
Quick Sort Algorithm Gyanblog I have been working on one of my programs related to the implementation of quick sort. the code below is a quick sort algorithm that selects the median of three elements as the pivot. but the thin. The space complexity of quicksort is listed as o(logn). however quicksort can process without use of any additional memory: at each iteration, during the partition process, the entries are sw. I have seen many places say quicksort is good because it fits to cache related stuff, such as said in wiki additionally, quicksort's sequential and localized memory references work well with a c. 9 being the recursion depth the maximum number of successive recursive calls before quicksort hits it´s base case, and noting that it (recursion depth) is a random variable, since it depends on the chosen pivot. what i want is to estimate the minimum possible and maximum possible recursion depth of quicksort. While quicksort always recursively descends into both partitions and original quickselect only descends into the one that contains the kth index, the algorithm for this problem should descend into a partition if and only if it contains one of the n g, 2*n g, (g 1)*n g array indexes the ones that are splitting points between grades. 2 currently the most advanced quicksort widely used is implemented in java's dualpivotquicksort.java so you can simply follow that approach and you will see a nice performance improvement: use insertion sort for small arrays (47 is the number used in java) use that dual pivot quicksort choosing the 2nd and 4th elements of 5 as the two pivots.

Quicksort Algorithm Interviewbit I have seen many places say quicksort is good because it fits to cache related stuff, such as said in wiki additionally, quicksort's sequential and localized memory references work well with a c. 9 being the recursion depth the maximum number of successive recursive calls before quicksort hits it´s base case, and noting that it (recursion depth) is a random variable, since it depends on the chosen pivot. what i want is to estimate the minimum possible and maximum possible recursion depth of quicksort. While quicksort always recursively descends into both partitions and original quickselect only descends into the one that contains the kth index, the algorithm for this problem should descend into a partition if and only if it contains one of the n g, 2*n g, (g 1)*n g array indexes the ones that are splitting points between grades. 2 currently the most advanced quicksort widely used is implemented in java's dualpivotquicksort.java so you can simply follow that approach and you will see a nice performance improvement: use insertion sort for small arrays (47 is the number used in java) use that dual pivot quicksort choosing the 2nd and 4th elements of 5 as the two pivots.

Quicksort Algorithm Interviewbit While quicksort always recursively descends into both partitions and original quickselect only descends into the one that contains the kth index, the algorithm for this problem should descend into a partition if and only if it contains one of the n g, 2*n g, (g 1)*n g array indexes the ones that are splitting points between grades. 2 currently the most advanced quicksort widely used is implemented in java's dualpivotquicksort.java so you can simply follow that approach and you will see a nice performance improvement: use insertion sort for small arrays (47 is the number used in java) use that dual pivot quicksort choosing the 2nd and 4th elements of 5 as the two pivots.
Comments are closed.