Quick Sort Using Recursion Theory Complexity Code

Free Video Quick Sort Using Recursion Theory Complexity Code From In this video, we cover the quick sort algorithm. including the theory, code implementation using recursion, space and time complexity analysis, along with comparison with merge sort. Quicksort is a sorting algorithm based on the divide and conquer that picks an element as a pivot and partitions the given array around the picked pivot by placing the pivot in its correct position in the sorted array.

Quicksort The Animation Of Recursion Dive into a comprehensive 42 minute video tutorial on quick sort using recursion. learn the theory behind the algorithm, understand its implementation in code, and analyze its space and time complexity. compare quick sort with merge sort and explore how in built sorting algorithms function. Quick sort is also a good example of a recursive algorithm. t (n) = t (k) t (n k 1) ? (n). t (k) > recursion relation for elements left of pivot. k is a number of element smaller than the pivot. t (k) > recursion relation for elements right of pivot. (n) > it is for partition process. Quick sort: a fast algorithm that improves time complexity using pivot based partitioning and recursion by carefully selecting pivots and structuring the array. Quicksort is a sorting algorithm based on the divide and conquer paradigm. in this algorithm the array is divided into two sub lists, one sub list will contain the smaller elements and another sub list will contain the larger elements and then these sub lists are sorted again using recursion.

Quicksort Complexity Quick sort: a fast algorithm that improves time complexity using pivot based partitioning and recursion by carefully selecting pivots and structuring the array. Quicksort is a sorting algorithm based on the divide and conquer paradigm. in this algorithm the array is divided into two sub lists, one sub list will contain the smaller elements and another sub list will contain the larger elements and then these sub lists are sorted again using recursion. Quicksort is an algorithm based on divide and conquer approach in which an array is split into sub arrays and these sub arrays are recursively sorted to get a sorted array. in this tutorial, you will understand the working of quicksort with working code in c, c , java, and python. In introduction to algorithms p169 it talks about using tail recursion for quicksort. the original quicksort algorithm earlier in the chapter is (in pseudo code) if (p < r) q: < partition(a, p, r) quicksort(a, p, q) quicksort(a, q 1, r) the optimized version using tail recursion is as follows. while (p < r) q: < partition(a, p, r). The time complexity of quick sort is o (n log n) on average case, but can become o (n^2) in the worst case. the space complexity of quick sort in the best case is o (log n), while in the worst case scenario, it becomes o (n) due to unbalanced partitioning causing a skewed recursion tree that requires a call stack of size o (n). Quick sort is a sorting algorithm that uses the divide and conquer technique. it picks a pivot element and puts it in the appropriate place in the sorted array. divide and conquer is a technique of breaking down the algorithms into subproblems, then solving the subproblems, and combining the results back together to solve the original problem.
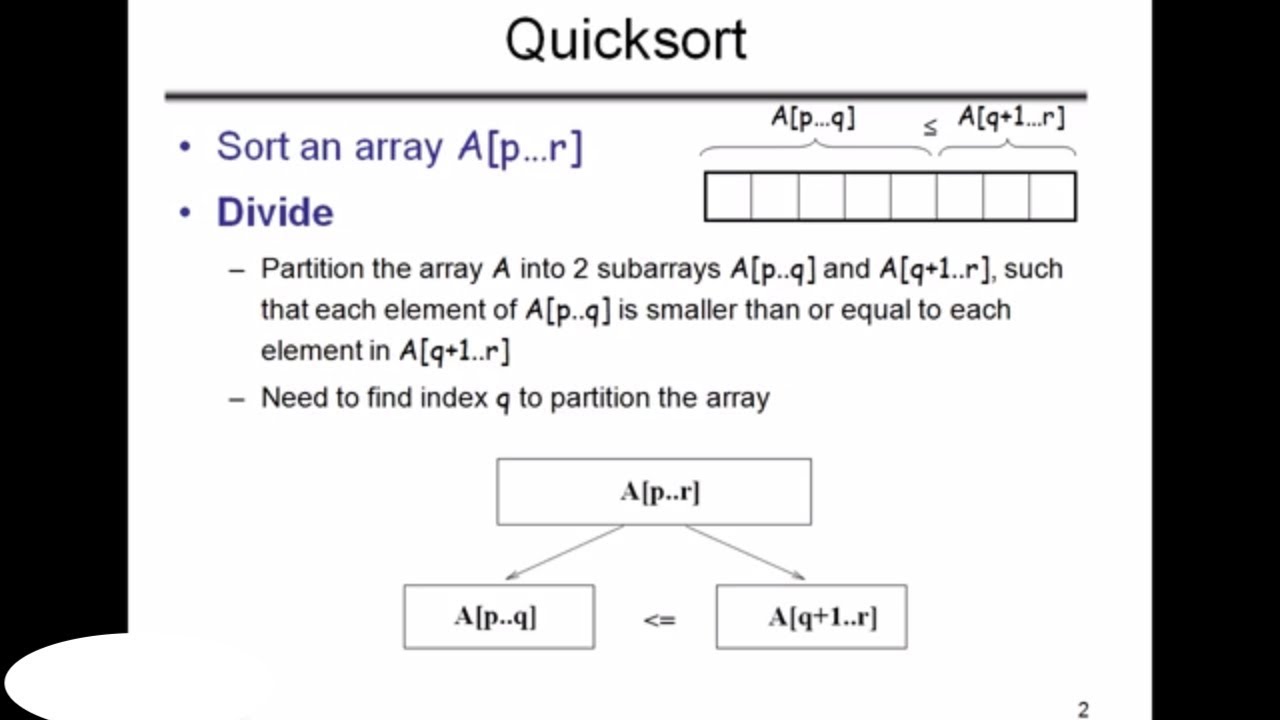
Quicksort Complexity Isro2014 62 Gate Overflow Quicksort is an algorithm based on divide and conquer approach in which an array is split into sub arrays and these sub arrays are recursively sorted to get a sorted array. in this tutorial, you will understand the working of quicksort with working code in c, c , java, and python. In introduction to algorithms p169 it talks about using tail recursion for quicksort. the original quicksort algorithm earlier in the chapter is (in pseudo code) if (p < r) q: < partition(a, p, r) quicksort(a, p, q) quicksort(a, q 1, r) the optimized version using tail recursion is as follows. while (p < r) q: < partition(a, p, r). The time complexity of quick sort is o (n log n) on average case, but can become o (n^2) in the worst case. the space complexity of quick sort in the best case is o (log n), while in the worst case scenario, it becomes o (n) due to unbalanced partitioning causing a skewed recursion tree that requires a call stack of size o (n). Quick sort is a sorting algorithm that uses the divide and conquer technique. it picks a pivot element and puts it in the appropriate place in the sorted array. divide and conquer is a technique of breaking down the algorithms into subproblems, then solving the subproblems, and combining the results back together to solve the original problem.

Quicksort Example In Java Using Recursion Sorting Algorithm The time complexity of quick sort is o (n log n) on average case, but can become o (n^2) in the worst case. the space complexity of quick sort in the best case is o (log n), while in the worst case scenario, it becomes o (n) due to unbalanced partitioning causing a skewed recursion tree that requires a call stack of size o (n). Quick sort is a sorting algorithm that uses the divide and conquer technique. it picks a pivot element and puts it in the appropriate place in the sorted array. divide and conquer is a technique of breaking down the algorithms into subproblems, then solving the subproblems, and combining the results back together to solve the original problem.
Comments are closed.