Question 4 Prove 1 2 3 2 3 4 N N 1 N 2 N N 1

Solved 3 Prove That For Any N 1 2 That Is в ђn в N Chegg Question 4: prove the following by using the principle of mathematical induction for all n ∈ n: 1.2.3 2.3.4 … n (n 1) (n 2) = (𝑛 (𝑛 1) (𝑛 2) (𝑛 3)) 4 let p (n): 1.2.3 2.3.4 … n (n 1) (n 2) = (𝑛 (𝑛 1) (𝑛 2) (𝑛 3)) 4 for n = 1, l.h.s = 1.2.3 = 6 r.h.s = (1 (1 1) (1 2) (1 3)) 4 = (1 ×. For all n ≥ 1 , prove that 1.2.3 2.3.4 ……… n (n 1) (n 2) = n(n 1)(n 2)(n 3) 4 n (n 1) (n 2) (n 3) 4. challenge your friends with exciting quiz games – click to play now! please log in or register to answer this question. p (1) = 1(1 1)(1 2)(1 3) 4 1 (1 1) (1 2) (1 3) 4 = 6 which is true.
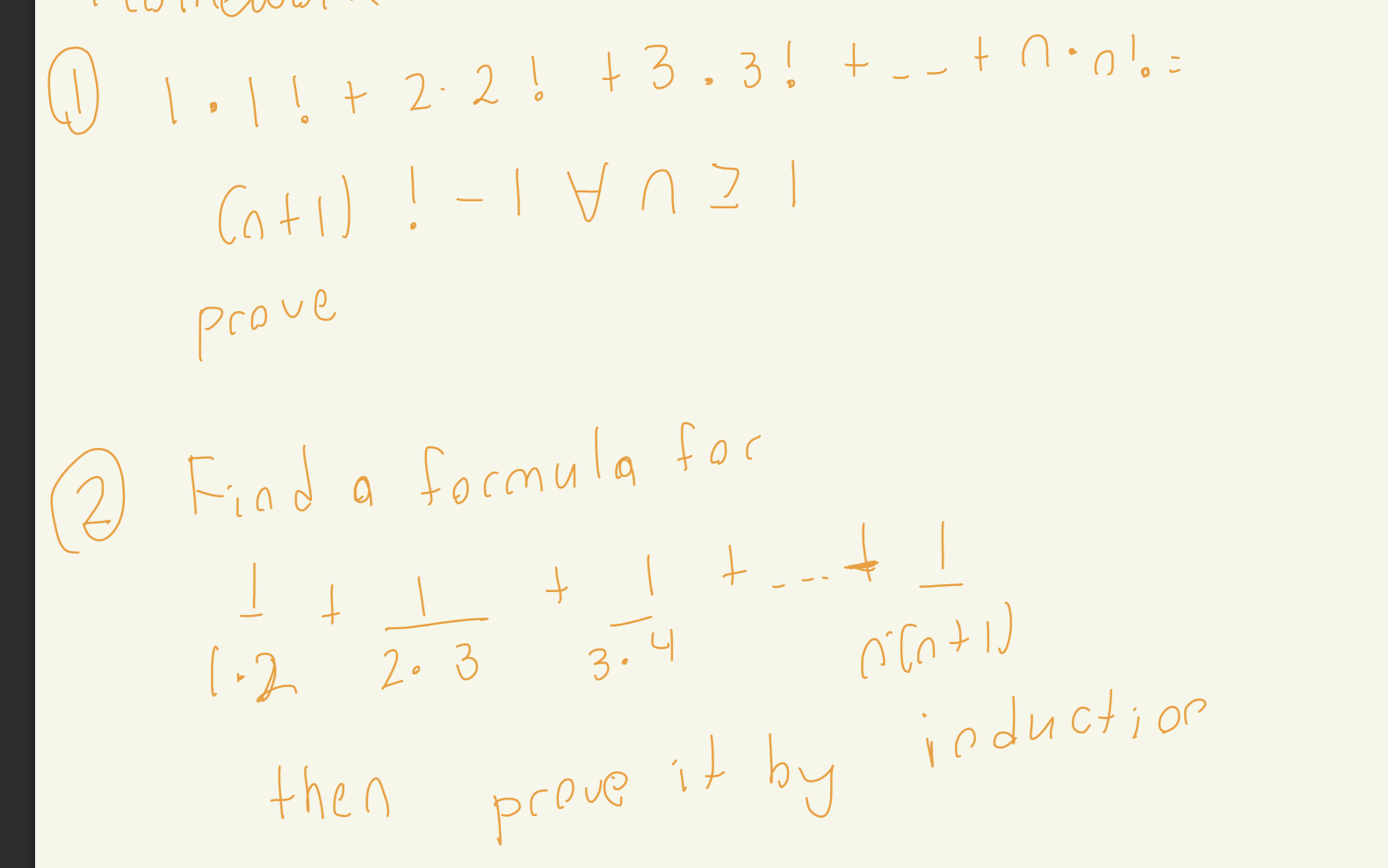
Solved Prove1тле1 2тле2 3тле3 Nтлеn N 1 1 Aтийтйе1prove 2 Chegg Prove by the principle of mathematical induction that 1 × 1! 2 × 2! 3 × 3! n × n! = (n 1)! – 1 for all natural numbers n. give an example of a statement p (n) which is true for all n. Using the principle of mathematical induction, prove that : 1.2.3 2.3.4 n(n 1)(n 2) = n(n 1)(n 2)(n 3) 4 for all n ∈ n . prove that 1 n 1 = ^ nc1 2 − 2(^ nc2) 3 3(^ nc3) 4 − (− 1)n 1n(^ ncn) n 1 . prove that n!(n 2) = n! (n 1)!. prove that .n c1 2 ×.nc2 3×.n c3 …. n×.ncn = n2n−1. We shall prove the result by principle of mathematical induction. rhs : 1 3 * 1 * 2 * 3 = 2. let us assume the result is true for n = k. we shall prove the result to be true for n = k 1. =rhs. hence the result holds for n=k 1. hence proof is complete by pmi and therefore the result holds. still have questions?. I have the following proof by induction question: $$ (1) (2) (2) (3) (3) (4) \cdots (n) (n 1) = \frac { (n) (n 1) (n 2)} {3} $$ can anybody tell me what i'm missing. this is where i've gone so far.

Question 5 Prove 1 3 2 32 3 33 N 3n 2n 1 3n 1 We shall prove the result by principle of mathematical induction. rhs : 1 3 * 1 * 2 * 3 = 2. let us assume the result is true for n = k. we shall prove the result to be true for n = k 1. =rhs. hence the result holds for n=k 1. hence proof is complete by pmi and therefore the result holds. still have questions?. I have the following proof by induction question: $$ (1) (2) (2) (3) (3) (4) \cdots (n) (n 1) = \frac { (n) (n 1) (n 2)} {3} $$ can anybody tell me what i'm missing. this is where i've gone so far. We have completed the basis step and the inductive step, so by mathematical induction we know that p (n) p (n) is true for all positive integers n n. that is, we have proven that 1 2 3 2 3 4 n (n 1) (n 2) = n (n 1) (n 2) (n 3) 4 1⋅ 2⋅3 2⋅3⋅4 n(n 1)(n 2) = 4n(n 1)(n 2)(n 3) for all positive integers n n. Here’s the best way to solve it. for n=1 l.h.s. 1*2 . ( up to 1 instance ) = 2 r.h.s. n (n 1) (n 2) 3 put n=1, so this equals to 1* (1 1) … not the question you’re looking for? post any question and get expert help quickly. By the principle of mathematical induction, prove 1.2 2.3 3.4 … n (n 1) = \ (\frac {n (n 1) (n 2)} {3}\), for all n ∈ n. These lessons help you brush up on important math topics and prepare you to dive into skill practice! learn algebra 1 skills for free! choose from hundreds of topics including functions, linear equations, quadratic equations, and more. start learning now!.
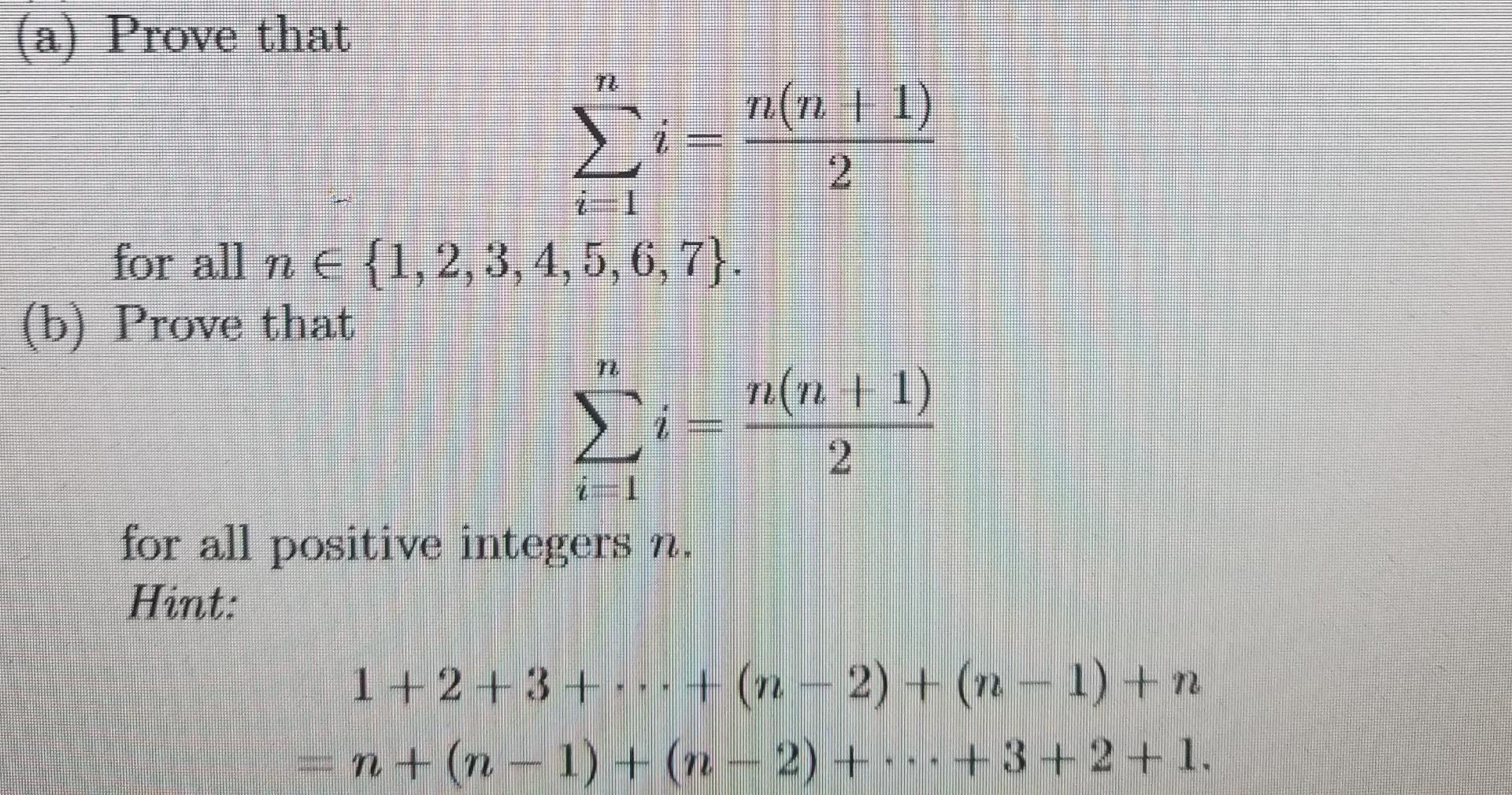
Solved A Prove That N N 1 σ 2 τι For All Ne 1 2 3 4 Chegg We have completed the basis step and the inductive step, so by mathematical induction we know that p (n) p (n) is true for all positive integers n n. that is, we have proven that 1 2 3 2 3 4 n (n 1) (n 2) = n (n 1) (n 2) (n 3) 4 1⋅ 2⋅3 2⋅3⋅4 n(n 1)(n 2) = 4n(n 1)(n 2)(n 3) for all positive integers n n. Here’s the best way to solve it. for n=1 l.h.s. 1*2 . ( up to 1 instance ) = 2 r.h.s. n (n 1) (n 2) 3 put n=1, so this equals to 1* (1 1) … not the question you’re looking for? post any question and get expert help quickly. By the principle of mathematical induction, prove 1.2 2.3 3.4 … n (n 1) = \ (\frac {n (n 1) (n 2)} {3}\), for all n ∈ n. These lessons help you brush up on important math topics and prepare you to dive into skill practice! learn algebra 1 skills for free! choose from hundreds of topics including functions, linear equations, quadratic equations, and more. start learning now!.

Question 11 Prove 1 1 2 3 1 2 3 4 1 3 4 5 1 N N 1 N 2 By the principle of mathematical induction, prove 1.2 2.3 3.4 … n (n 1) = \ (\frac {n (n 1) (n 2)} {3}\), for all n ∈ n. These lessons help you brush up on important math topics and prepare you to dive into skill practice! learn algebra 1 skills for free! choose from hundreds of topics including functions, linear equations, quadratic equations, and more. start learning now!.
Comments are closed.