Primitive Data Types In Typescript 4 Typescript Primitivedatatypes Programming Typesystem

Lesson 04 Primitive Data Types I Pdf Data Type Variable Find all the primitive roots of 13 13 my attempt: since that 13 13 is a prime i need to look for g g such that g13−1 ≡ 1 (mod 13) g 13 1 ≡ 1 (mod 13) there are ϕ(12) = 4 ϕ (12) = 4 classes modulo 12 12 how can i find the classes?. How to find all primitive triples when one value of (a, b, c) (a, b, c) is given? for example in this case a = 45 a = 45. what is the procedure to find the primitive triples ? conditions for primitive triples are: a2 b2 = c2 a 2 b 2 = c 2 (a, b) = 1 (a, b) = 1 a a and c c are odd and b b is even.

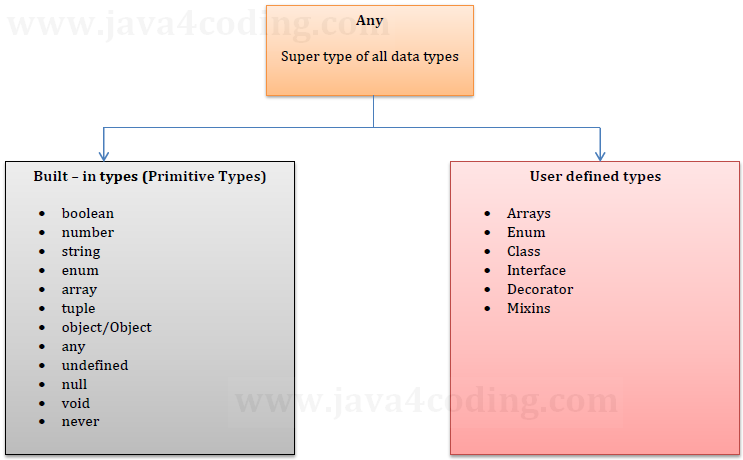
Typescript Data Types Java4coding By the multiplication principle, it thus follows that there are at least ϕ(p − 1) ϕ (p 1) primitive roots modulo p p. we will show that these are in fact the only primitive roots. Primitive recursion does allow the "next step provider" h h to see both inputs and the previous value, but we don't need to use that information. in most natural examples i think we don't in fact need that. finally, it may also help to go in the opposite direction: given a g g and h h, try to compute the first few values of the resulting f f. I'm trying to understand what primitive roots are for a given mod n mod n. wolfram's definition is as follows: a primitive root of a prime p p is an integer g g such that g (mod p) g (mod p) has multiplicative order p − 1 p 1 the main thing i'm confused about is what "multiplicative order" is. also, for the notation g (mod p) g (mod p), is it saying g g times mod p mod p or does it have. 14 there is another example of a non primitive recursive but total computable function that explains better what the restricted definition of primitive recursion entails. each primitive recursive function is defined by a particular finite set of recursion equations, in terms of a fixed set of basic functions.

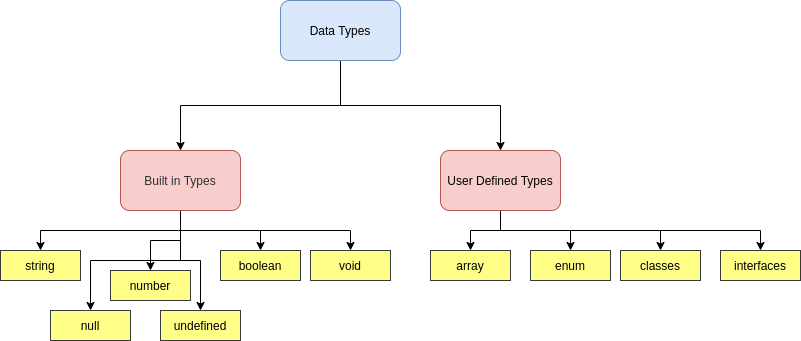
Primitive Data Type Type Script Tutorials Code Topology I'm trying to understand what primitive roots are for a given mod n mod n. wolfram's definition is as follows: a primitive root of a prime p p is an integer g g such that g (mod p) g (mod p) has multiplicative order p − 1 p 1 the main thing i'm confused about is what "multiplicative order" is. also, for the notation g (mod p) g (mod p), is it saying g g times mod p mod p or does it have. 14 there is another example of a non primitive recursive but total computable function that explains better what the restricted definition of primitive recursion entails. each primitive recursive function is defined by a particular finite set of recursion equations, in terms of a fixed set of basic functions. Do holomorphic functions have primitive? ask question asked 3 years, 3 months ago modified 3 years, 3 months ago. Since r r is a primitive root of p p, it follows that r r is a quadratic non residue of p p. thus by euler's criterion, we have r2k ≡ −1 (mod p) r 2 k ≡ 1 (mod p). Prove if n n has a primitive root, then it has exactly ϕ(ϕ(n)) ϕ (ϕ (n)) of them. let a a be the primitive root then i know other primitive roots will be among {a,a2,a3 ⋯ ⋯aϕ(n)} {a, a 2, a 3 a ϕ (n)} because any other number will be congruent modulo n n to one of these. Answers to the question of the integral of 1 x are all based on an implicit assumption that the upper and lower limits of the integral are both positive real numbers. if we allow more generality, we find an interesting paradox. for instance, suppose the limits on the integral are from a to a where a is a real, positive number. the posted answer in term of ln would give ln (a) ln (a) = ln (a.

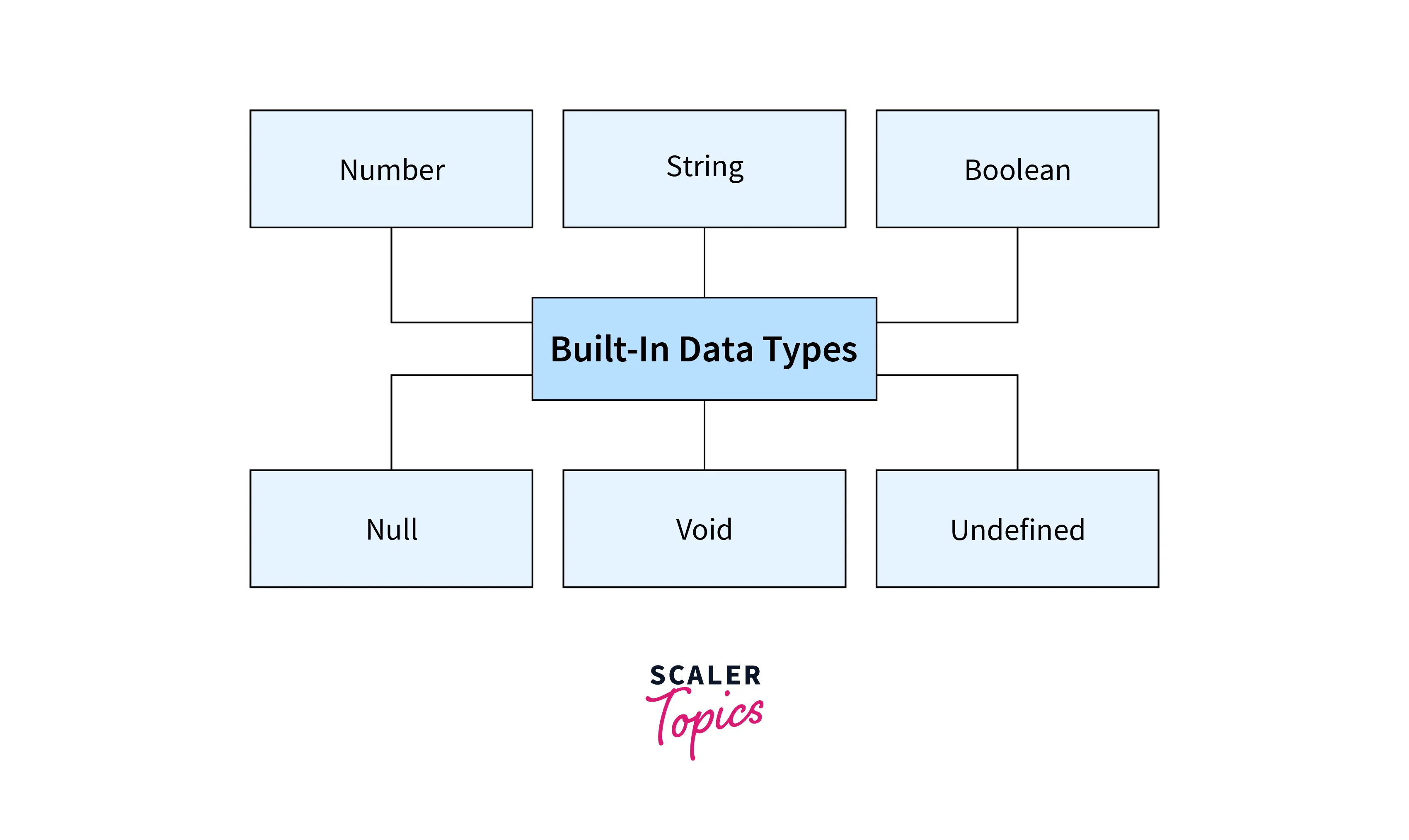
Built In Types In Typescript Scaler Topics Do holomorphic functions have primitive? ask question asked 3 years, 3 months ago modified 3 years, 3 months ago. Since r r is a primitive root of p p, it follows that r r is a quadratic non residue of p p. thus by euler's criterion, we have r2k ≡ −1 (mod p) r 2 k ≡ 1 (mod p). Prove if n n has a primitive root, then it has exactly ϕ(ϕ(n)) ϕ (ϕ (n)) of them. let a a be the primitive root then i know other primitive roots will be among {a,a2,a3 ⋯ ⋯aϕ(n)} {a, a 2, a 3 a ϕ (n)} because any other number will be congruent modulo n n to one of these. Answers to the question of the integral of 1 x are all based on an implicit assumption that the upper and lower limits of the integral are both positive real numbers. if we allow more generality, we find an interesting paradox. for instance, suppose the limits on the integral are from a to a where a is a real, positive number. the posted answer in term of ln would give ln (a) ln (a) = ln (a.

Typescript Data Types Tutlane Prove if n n has a primitive root, then it has exactly ϕ(ϕ(n)) ϕ (ϕ (n)) of them. let a a be the primitive root then i know other primitive roots will be among {a,a2,a3 ⋯ ⋯aϕ(n)} {a, a 2, a 3 a ϕ (n)} because any other number will be congruent modulo n n to one of these. Answers to the question of the integral of 1 x are all based on an implicit assumption that the upper and lower limits of the integral are both positive real numbers. if we allow more generality, we find an interesting paradox. for instance, suppose the limits on the integral are from a to a where a is a real, positive number. the posted answer in term of ln would give ln (a) ln (a) = ln (a.

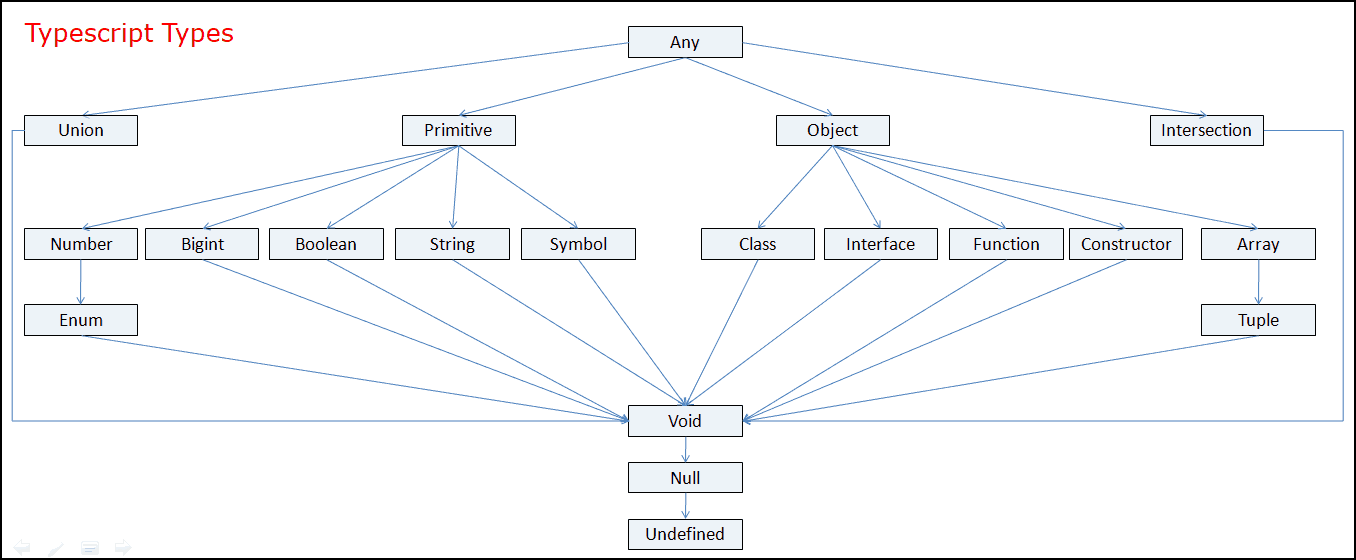
Typescript Data Types Tektutorialshub