Order Of Growth Of An Algorithm Codersathi

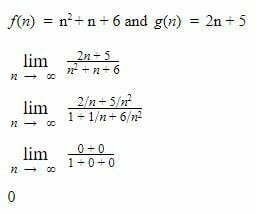
Order Of Growth Of An Algorithm Codersathi Order of growth of an algorithm is a way of predicting how long is the execution time of a program and the space memory is required when the input size changes. we can have multiple solutions and need to determine the most efficient one to use. F (n) has higher order of growth as it grows quadratically in terms of input size. how do we quickly find order of growth? when n >= 0, f (n) >= 0 and g (n) >= 0, we can use the below steps. ignore the order terms. ignore the constants for example, example 1 : 4n2 3n 100 after ignoring lower order terms, we get 4n2 after ignoring constants.

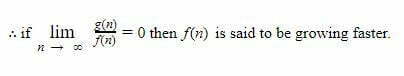
Order Of Growth Of An Algorithm Codersathi Common order of growth classifications definition. if f (n) ~ c g(n) for some constant c > 0, then the order of growth of f (n) is g(n). ・ignores leading coefficient.・ignores lower order terms. ex. the order of growth of the running time of this code is n 3. Let f, g : n → r be real valued functions on n. we say that f is of order g, written o (g), if there exists a constant c ∈ r such that f (n) ≤ c g (n) for every n ∈ n. in simpler terms? the. Different types of order of growth of an algorithm we come across in this course are shown below. the terms order of growth, the efficiency of an algorithm, or the number of steps executed by an algorithm means the same. the constant order of growth means the number of steps executed by the algorithm is constant, whatever the input may be. When an algorithm contains a recursive call to itself, we can often describe its running time by a recurrence equation, which describes the overall running time on a problem of size n in terms of.

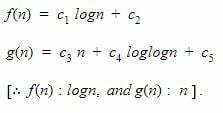
Order Of Growth Of An Algorithm Codersathi Different types of order of growth of an algorithm we come across in this course are shown below. the terms order of growth, the efficiency of an algorithm, or the number of steps executed by an algorithm means the same. the constant order of growth means the number of steps executed by the algorithm is constant, whatever the input may be. When an algorithm contains a recursive call to itself, we can often describe its running time by a recurrence equation, which describes the overall running time on a problem of size n in terms of. The order of growth of an algorithm is an approximation of the time required to run a computer program as the input size increases. the order of growth ignores the constant factor needed for fixed operations and focuses instead on the operations that increase proportional to input size. There are 5 main orders of growth, each describing how fast a function's runtime grows, as its inputs get bigger. we use the symbol theta to denote an order of growth. constant growth. logarithmic growth. linear growth. quadratic growth. exponential growth. Asymptotic analysis is a technique to measure the order of growth of time taken by a program based on the input size. Time complexity order of growth defines the amount of time taken by any program with respect to the size of the input. time complexity specifies how the program would behave as the order of size of input is increased.

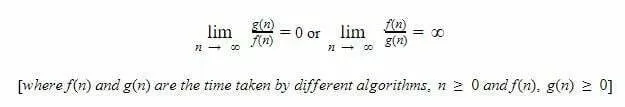
Order Of Growth Of An Algorithm Codersathi The order of growth of an algorithm is an approximation of the time required to run a computer program as the input size increases. the order of growth ignores the constant factor needed for fixed operations and focuses instead on the operations that increase proportional to input size. There are 5 main orders of growth, each describing how fast a function's runtime grows, as its inputs get bigger. we use the symbol theta to denote an order of growth. constant growth. logarithmic growth. linear growth. quadratic growth. exponential growth. Asymptotic analysis is a technique to measure the order of growth of time taken by a program based on the input size. Time complexity order of growth defines the amount of time taken by any program with respect to the size of the input. time complexity specifies how the program would behave as the order of size of input is increased.