Lecture 2 2d Finite Element Analysis

A Finite Element Analysis Pdf Stress Mechanics 3 D Computer #fea #twodimensional #analysis in the second lecture of this series on 2d finite element analysis we cover the basics of the theory of elasticity as applicable to the fea. … more. In order to be able to take the integrals numerically using gq integration we need to introduce 2d master elements and be able to work with master element coordinates.

Me2353 Finite Element Analysis Lecture Notes Pdf Www In order to derive the fundamental concepts of fem we will start by looking at an extremely simple ode and approximate it using fem. 1.1 the model problem. the model problem is: −u′′ u= x 0

Finite Element Analysis Of A 2 D Linear Static Structure Flat Plate Read the input data description for fem2d to know the meaning of all input variables; other variables are described below. save the previous iteration solution and update the current one. test for the convergence of the solution. initialize the arrays. do loops on numerical. integration begin here. subroutine interpln2d. is called here. Review of the basic theory in 2 d elasticity. lecture 2. stiffness matrices for 2 d problems; t3 element. lecture 3. t6, q4 and q8 elements; example. Finite element method: introducing approximations of trial solution and weight function into the weak form (for all we that we = 0 on Γt ), we obtain the following equation, where the integrals of the weak form are transferred into the sum of integrals in elements:. The theory of finite element analysis (fea) essentially involves solving the spring equation, f = kδ, at a large scale. there are several basic steps in the finite element method: discretize the structure into elements. these elements are connected to one another via nodes. determine a local stiffness matrix for each element. The solution of 2d differential equations using the finite element method is discussed. weak formulation is employed to reduce the order, jacobian matrix is introduced and used to find differential terms, and elemental matrices are obtained under various assumptions. Parameterize by adding degrees of freedom at element midpoints. each element then has three local nodes: xk 1; xk 2; xk 3, and three local basis functions hk 1(x); hk 2(x); hk 3(x).

2d Vs 3d Finite Element Analysis With Examples Enterfea 55 Off Finite element method: introducing approximations of trial solution and weight function into the weak form (for all we that we = 0 on Γt ), we obtain the following equation, where the integrals of the weak form are transferred into the sum of integrals in elements:. The theory of finite element analysis (fea) essentially involves solving the spring equation, f = kδ, at a large scale. there are several basic steps in the finite element method: discretize the structure into elements. these elements are connected to one another via nodes. determine a local stiffness matrix for each element. The solution of 2d differential equations using the finite element method is discussed. weak formulation is employed to reduce the order, jacobian matrix is introduced and used to find differential terms, and elemental matrices are obtained under various assumptions. Parameterize by adding degrees of freedom at element midpoints. each element then has three local nodes: xk 1; xk 2; xk 3, and three local basis functions hk 1(x); hk 2(x); hk 3(x).
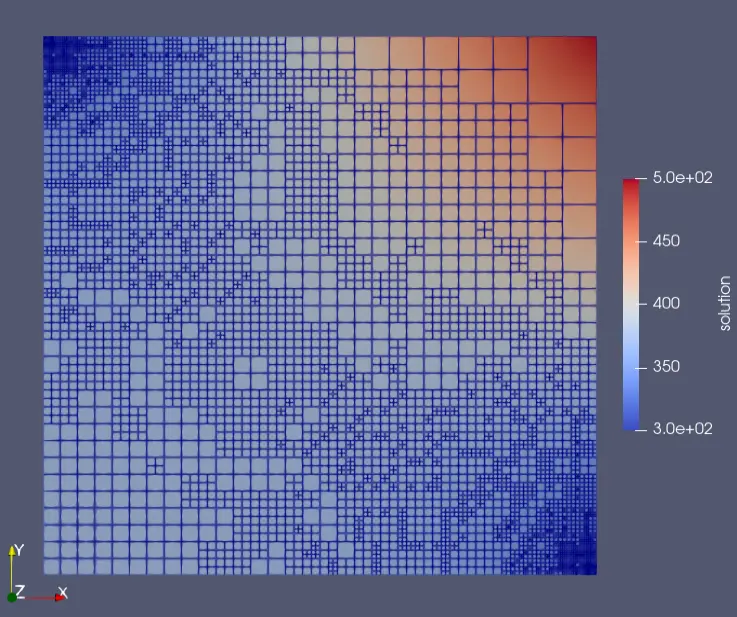
2d Finite Element Analysis Bartu Kurtulus The solution of 2d differential equations using the finite element method is discussed. weak formulation is employed to reduce the order, jacobian matrix is introduced and used to find differential terms, and elemental matrices are obtained under various assumptions. Parameterize by adding degrees of freedom at element midpoints. each element then has three local nodes: xk 1; xk 2; xk 3, and three local basis functions hk 1(x); hk 2(x); hk 3(x).
Comments are closed.