In The Following Exercises Change The Order Of Integration And Evaluate The Integral %e2%88%ab_01

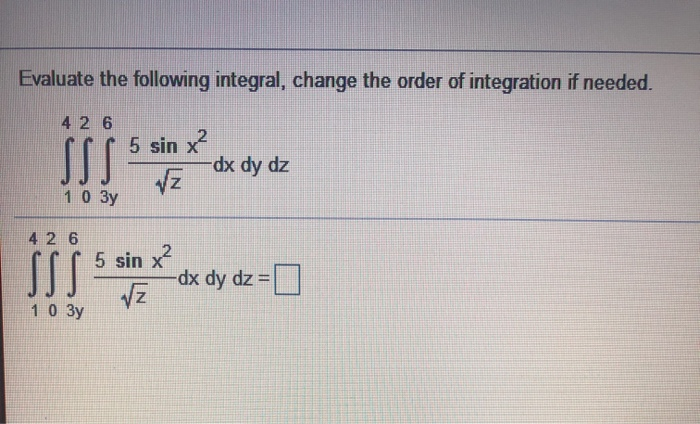
Solved Evaluate The Following Integral Change The Order Of Chegg As for double integrals we de ̄ne the integral of f over a more general bounded region e by ̄nding a large box b containing e and integrating the function that is equal to f in e and 0 outside e over the lager box b. To start the solution to this problem, observe that the order of integration is dydx in the given integral ∫ − 1 π 2 ∫ 0 x 1 sin x d y d x.

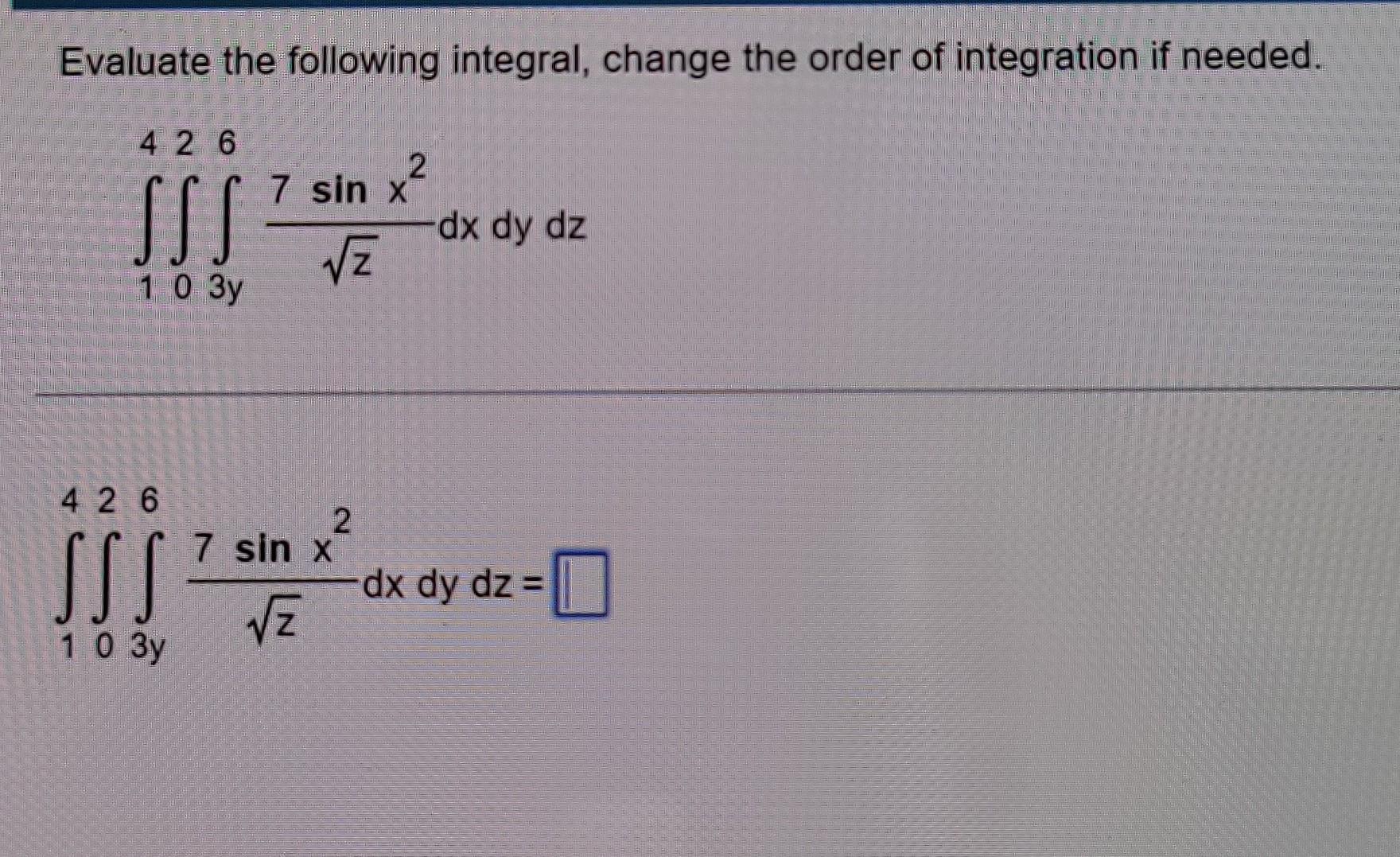
Solved Evaluate The Following Integral Change The Order Of Chegg In the following exercises, change the order of integration and evaluate the integral. ∫ 0^1… dave anderson 158 subscribers subscribe. We use these to sketch the region of integration. the given limits have inner variable y. to reverse the order of integration we use horizontal stripes. the limits in this order are (inner) x from 0 to y; (outer) y from 0 to π 2. so the integral becomes π 2 y sin y. = sin y. = 1. In the following integrals, change the order of integration, sketch the corresponding regions, and evaluate the integral both ways (a) \displaystyle \int { 0 } ^ { 1 } \int { x } ^ { 1 } x y d y d x ∫ 01∫ x1 xydydx (b) \displaystyle \int { 0 } ^ { \pi 2 } \int { 0 } ^ { \cos \theta } \cos \theta d r d \theta ∫ 0π 2∫ 0cosθ. When we change the order of integration, x will integrate first. from the region description, y varies from 0 to x, so the new limits of y should be from 0 to x, and x will still vary from 0 to 1. with the new order of integration, the integral becomes: ∫ 0 1 ∫ 0 x sin (x 2) d y d x.

Solved Evaluate The Following Integral Change The Order Of Chegg In the following integrals, change the order of integration, sketch the corresponding regions, and evaluate the integral both ways (a) \displaystyle \int { 0 } ^ { 1 } \int { x } ^ { 1 } x y d y d x ∫ 01∫ x1 xydydx (b) \displaystyle \int { 0 } ^ { \pi 2 } \int { 0 } ^ { \cos \theta } \cos \theta d r d \theta ∫ 0π 2∫ 0cosθ. When we change the order of integration, x will integrate first. from the region description, y varies from 0 to x, so the new limits of y should be from 0 to x, and x will still vary from 0 to 1. with the new order of integration, the integral becomes: ∫ 0 1 ∫ 0 x sin (x 2) d y d x. Change the order of integration: ∫ 04∫ 0 4−y 4−yxe2y dxdy. evaluate the inner integral: ∫ 0 4−y xdx= [2x2]04−y = 24−y. substitute the result back into the integral: ∫ 04 2(4−y)(4−y)e2y dy =∫ 04 2e2y dy. evaluate the integral: ∫ 2e2y dy = 41e2y c, so we evaluate from 0 to 4: [41e2y]04 = 41(e8−1). thus, the final answer is: 41(e8−1). 41(e8−1). The key steps are: 1) draw a sketch of the region of integration to determine the new limits. 2) when changing the order, the lower limit of one variable becomes the upper limit of the other variable and vice versa. There are 2 steps to solve this one. this ai generated tip is based on chegg's full solution. sign up to see more! sketch the region of integration for the given integral. in the following exercises, change the order of integration and evaluate the integral. 2 x 1 96. sin xdy dx 1 0 11 x 97. xdy dx 0 x dxdy 98. In this video, we simplify the concept of changing the order of integration in double integrals. you'll learn: ️ why we change the order of integration ️ ste.

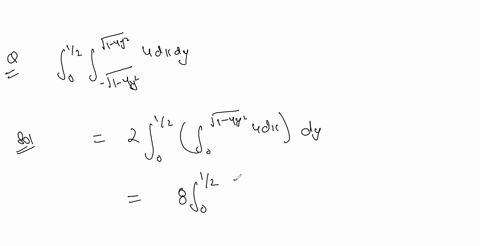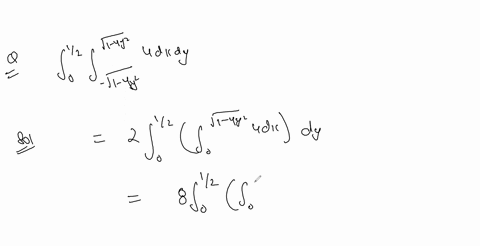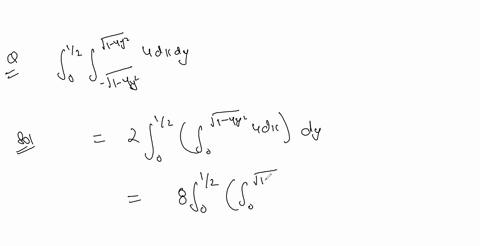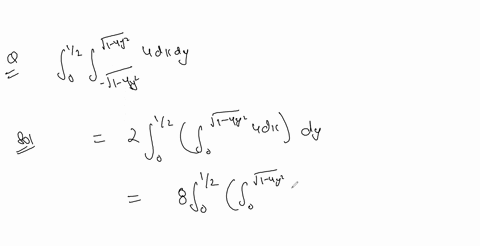
Solved In The Following Exercises Change The Order Of Integration And Change the order of integration: ∫ 04∫ 0 4−y 4−yxe2y dxdy. evaluate the inner integral: ∫ 0 4−y xdx= [2x2]04−y = 24−y. substitute the result back into the integral: ∫ 04 2(4−y)(4−y)e2y dy =∫ 04 2e2y dy. evaluate the integral: ∫ 2e2y dy = 41e2y c, so we evaluate from 0 to 4: [41e2y]04 = 41(e8−1). thus, the final answer is: 41(e8−1). 41(e8−1). The key steps are: 1) draw a sketch of the region of integration to determine the new limits. 2) when changing the order, the lower limit of one variable becomes the upper limit of the other variable and vice versa. There are 2 steps to solve this one. this ai generated tip is based on chegg's full solution. sign up to see more! sketch the region of integration for the given integral. in the following exercises, change the order of integration and evaluate the integral. 2 x 1 96. sin xdy dx 1 0 11 x 97. xdy dx 0 x dxdy 98. In this video, we simplify the concept of changing the order of integration in double integrals. you'll learn: ️ why we change the order of integration ️ ste.

Solved 6 In The Following Exercises Change The Order There are 2 steps to solve this one. this ai generated tip is based on chegg's full solution. sign up to see more! sketch the region of integration for the given integral. in the following exercises, change the order of integration and evaluate the integral. 2 x 1 96. sin xdy dx 1 0 11 x 97. xdy dx 0 x dxdy 98. In this video, we simplify the concept of changing the order of integration in double integrals. you'll learn: ️ why we change the order of integration ️ ste.