How To Prove Or Disprove Big O Introduction To Computer Science

Big O Mit Pdf Pdf Time Complexity Areas Of Computer Science In this video, i will show you how to prove or disprove big o. i will also go over the formal definition of the formula big o using asymptotic notation to determine the runtime of an. Big o notation is a mathematical notation used to find an upper bound on time taken by an algorithm or data structure. it provides a way to compare the performance of different algorithms and data structures, and to predict how they will behave as the input size increases.
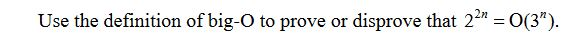
Solved Use The Definition Of Big O To Prove Or Disprove Chegg To build a proof for a "for all" statement, pretend someone just handed you specific values. be careful you make no implicit assumptions about their properties (you can explicitly state properties, such as n > 0). in the case of proving big o, you need to find the c and n. showing |g (n)| ≤ c|f (n)| for a single n isn't sufficent. In general, for any p(n) p (n) and q(n) q (n), to show p(n) p (n) is not o(q(n) o (q (n), we need to show that for any c c, p(n) p (n) is > cq(n)> c q (n) for arbitrarily large values of n n. Big o is the way we analyze how efficient algorithms are (or code in this case) without getting too mired in the details. we can model how much time any function is going to take given n inputs (think an array of length n), but in reality we're interested in the order of magnitude of the number and not necessarily of the exact figure. Explain intuition behind their definitions. prove one function is big o omega theta of another function. simplify algebraic expressions using the rules of asymptotic analysis. list common asymptotic complexity orders, and how they compare. work some examples.

Solved 1 5 A In Computer Science We Used Big O What Chegg Big o is the way we analyze how efficient algorithms are (or code in this case) without getting too mired in the details. we can model how much time any function is going to take given n inputs (think an array of length n), but in reality we're interested in the order of magnitude of the number and not necessarily of the exact figure. Explain intuition behind their definitions. prove one function is big o omega theta of another function. simplify algebraic expressions using the rules of asymptotic analysis. list common asymptotic complexity orders, and how they compare. work some examples. The way to solve this is to create a function t (n) that measures the runtime of the function and figure out the big o notation for it. to solve a problem of size n, i must solve a problem of size n 1. The big o notation is called "asymptotic" complexity because "asymptote" means what happens as n n gets very large. we don't worry much about values of n n, since in computer science we're usually dealing with thousands, millions, or billions of items of data. Big o notation is an efficient way to evaluate algorithm performance. the study of the performance of algorithms – or algorithmic complexity – falls into the field of algorithm analysis. this method calculates the resources (e.g., disk space or time) needed to solve the assigned problem. As a homework assignment i have been given several assignments along the following: let f (n) and g (n) be asymptotically positive functions. prove or disprove each of the following conjectures. now, my real question is how would you go about proving this in a formal way?.

Unraveling Big O Notation Calculation In Computer Science Algorithm The way to solve this is to create a function t (n) that measures the runtime of the function and figure out the big o notation for it. to solve a problem of size n, i must solve a problem of size n 1. The big o notation is called "asymptotic" complexity because "asymptote" means what happens as n n gets very large. we don't worry much about values of n n, since in computer science we're usually dealing with thousands, millions, or billions of items of data. Big o notation is an efficient way to evaluate algorithm performance. the study of the performance of algorithms – or algorithmic complexity – falls into the field of algorithm analysis. this method calculates the resources (e.g., disk space or time) needed to solve the assigned problem. As a homework assignment i have been given several assignments along the following: let f (n) and g (n) be asymptotically positive functions. prove or disprove each of the following conjectures. now, my real question is how would you go about proving this in a formal way?.
Comments are closed.