Graphing An Inequality Dashed Or Solid Line Where Do I Add Shading

Solved When Graphing A Linear Inequality Which Of The Chegg Hey algebra students! if you are wondering how to graph an inequality, whether to make a dashed or solid line, and where to shade your graph — this video is. How to graph a linear inequality graph the "equals" line, then shade in the correct area. follow these steps: rearrange the equation so "y" is on the left and everything else on the right. plot the " y= " line (make it a solid line for y≤ or y≥, and a dashed line for y< or y>) shade above the line for a "greater than" (y> or y≥).

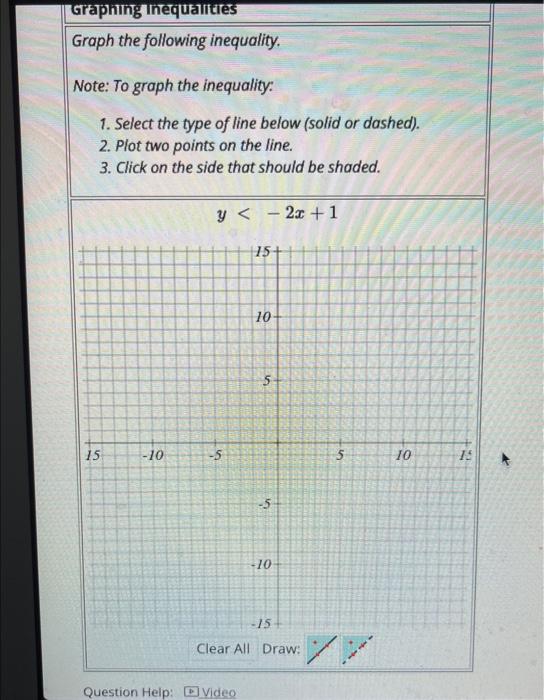
Solved Graph The Following Inequality Note To Graph The Chegg This step by step guide on graphing linear inequalities will show you how to graph a linear inequality on the coordinate plane. the guide will review when to use a solid or dotted line as well as when to shade above or below the line when graphing linear inequalities and determining the solution set. As shown in this image, the first step will be to determine whether you will use a solid boundary line or a dashed boundary line. the inequality symbol will help you to determine the boundary line. if the inequality symbol is greater than or less than, then you will use a dotted boundary line. With inequalities, you can add colored shading to your desmos graph. use strict inequalities (<< and >>) for dotted lines and non strict inequalities (≤ ≤ and ≥ ≥) for solid lines. Use dashed or dotted line if you have the strict inequality symbols which are > > > and < < <. use solid line if you have non strict inequality symbols which are ≥ \ge ≥ and ≤ \le ≤.

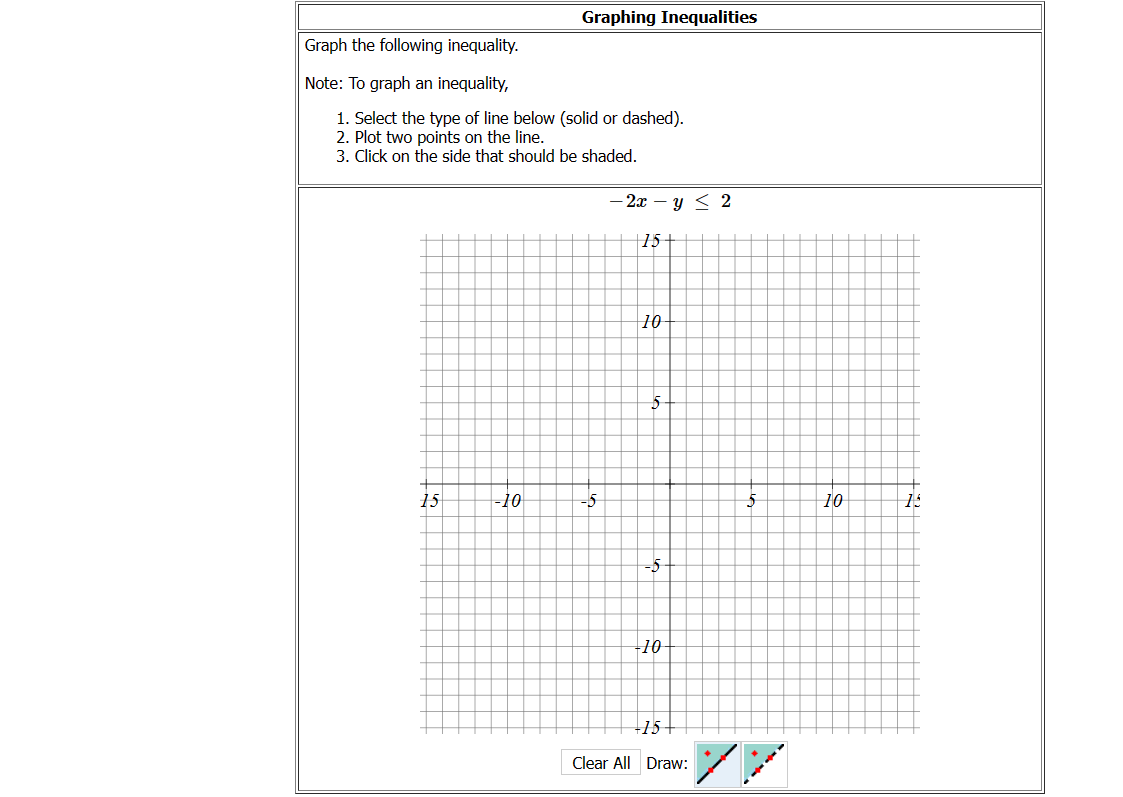
Solved Graph The Following Inequality Note To Graph An Chegg With inequalities, you can add colored shading to your desmos graph. use strict inequalities (<< and >>) for dotted lines and non strict inequalities (≤ ≤ and ≥ ≥) for solid lines. Use dashed or dotted line if you have the strict inequality symbols which are > > > and < < <. use solid line if you have non strict inequality symbols which are ≥ \ge ≥ and ≤ \le ≤. For graphing inequalities, we treat the inequality symbols ‘≥’ and ‘≤’ as ‘=’ and then graph the resulting equation. for such an equation with inequalities ≥’ or ‘≤’, the graph forms a solid line, whereas if the inequality is ‘<’ or ‘>,’ it is graphed as a dotted line. Use a solid line for < or > to show that the points on the line are included. use a dashed line for < or > to show that the points on the line are not included. Graph the inequality as if it was an equation. determine if the line or curve should be solid or dashed. test a point off of the line or curve to determine if it is point within the shaded region. shade the correct region. use the examples below to help understand how these steps are accomplished. For this scenario, we graph our boundary line as a solid line. this indicates that points on the line will satisfy the inequality. this will be our boundary line. we need to note that this is a strict inequality. the boundary line will be a dashed line.

Solved Graph The Following Inequality Note To Graph The Chegg For graphing inequalities, we treat the inequality symbols ‘≥’ and ‘≤’ as ‘=’ and then graph the resulting equation. for such an equation with inequalities ≥’ or ‘≤’, the graph forms a solid line, whereas if the inequality is ‘<’ or ‘>,’ it is graphed as a dotted line. Use a solid line for < or > to show that the points on the line are included. use a dashed line for < or > to show that the points on the line are not included. Graph the inequality as if it was an equation. determine if the line or curve should be solid or dashed. test a point off of the line or curve to determine if it is point within the shaded region. shade the correct region. use the examples below to help understand how these steps are accomplished. For this scenario, we graph our boundary line as a solid line. this indicates that points on the line will satisfy the inequality. this will be our boundary line. we need to note that this is a strict inequality. the boundary line will be a dashed line.