Fea Of Beam Structures Pdf Finite Element Method Mathematics

Fea Of Beam Structures Pdf Finite Element Method Mathematics Determine the critical buckling load of an axially loaded long slender bar of length with hinged ends. the bar has a square cross section with width and height set to 0.5 inches. Application of the finite element method. most researchers agree that the era of the finite element method begins with a lecture presented in 1941 by r. courant4 to the american a. sociation for the advancement of science. in his work, courant used the ritz method and introduced the pivotal concept of spatial discretization for the .

Implementation Of A Beam Element In Fea Using Matlab Type The The finite element method (fem), or finite element analysis (fea), is a computational technique used to obtain approximate solutions of boundary value problems in engineering. With the development of finite element method, together with tremendous increases in computing power and convenience, today it is possible to understand structural behavior with levels of accuracy. Finite element analysis is implemented to approximate the beam deflection. cubic shape functions are used. the numerical results agree with the analytical results. Finite element method for beams is very similar to the geometry of a bar. it is also geometrically a bar of an arbitrary cross section, by bar it is meant that one of the dimensions is considerably larger than the other two, whose primary unction is to support transverse loading. the main difference between the beam and the tr.

Pdf Finite Element Formulation For Beam Element Finite element analysis is implemented to approximate the beam deflection. cubic shape functions are used. the numerical results agree with the analytical results. Finite element method for beams is very similar to the geometry of a bar. it is also geometrically a bar of an arbitrary cross section, by bar it is meant that one of the dimensions is considerably larger than the other two, whose primary unction is to support transverse loading. the main difference between the beam and the tr. Continuity requirement based on the weak form, which requires that the second derivative of w exists and square integrable. continuity based on the primary variables, which requires carrying w and its first derivative as the nodal variables, requires cubic approximation w. Beam element w axial stiffness • if we combine the bar and beam stiffness matrices, we get a general beam stiffness matrix with axial stiffness. Finite element analysis (fea) involves the practical application of the finite element method to solve a real world problem. why is fea helpful? but, we’d like a way to estimate stresses and deformations in engineering components and structures. fea, when used correctly, can help!. This document discusses finite element analysis for beams. it explains that beams require a different treatment than other structural elements due to their thin dimensions.
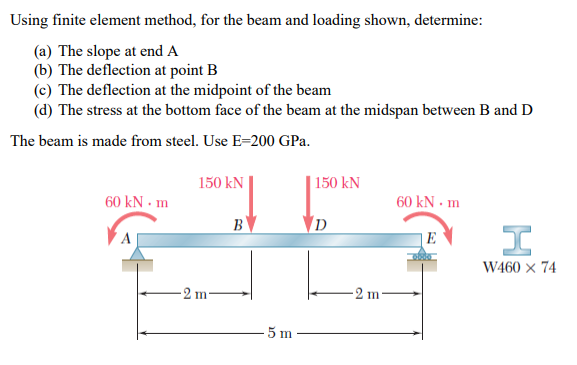
Solved Using Finite Element Method For The Beam And Loading Chegg Continuity requirement based on the weak form, which requires that the second derivative of w exists and square integrable. continuity based on the primary variables, which requires carrying w and its first derivative as the nodal variables, requires cubic approximation w. Beam element w axial stiffness • if we combine the bar and beam stiffness matrices, we get a general beam stiffness matrix with axial stiffness. Finite element analysis (fea) involves the practical application of the finite element method to solve a real world problem. why is fea helpful? but, we’d like a way to estimate stresses and deformations in engineering components and structures. fea, when used correctly, can help!. This document discusses finite element analysis for beams. it explains that beams require a different treatment than other structural elements due to their thin dimensions.
Comments are closed.