Ex Infinite Series Limit Comparison Test Geometric Divergent This video provides an example of how to apply the limit comparison test to determine if an infinite series is convergent, divergent, or if the test is inconclusive. In this section we will discuss using the comparison test and limit comparison tests to determine if an infinite series converges or diverges. in order to use either test the terms of the infinite series must be positive. proofs for both tests are also given.
Ex Infinite Series Limit Comparison Test Divergent Physics Here's the limit comparison test from an online source: limn→∞ an bn = c lim n → ∞ a n b n = c. where an a n and bn b n are the general terms of two different infinite series. if c c is finite and positive, both infinite series will converge or both will diverge. a series will converge diverge based on its behaviour as n n approaches ∞ ∞. Suppose ∑ n = 0 ∞ a n is divergent, and there are sequences {b n} and {c n} such that 0 ≤ b n ≤ a n ≤ c n for all n. what can be said about the series ∑ n = 0 ∞ b n and ∑ n = 0 ∞ c n?. Take bn = 1 5n b n = 1 5 n. the series ∑∞ n=1 bn = ∑∞ n=1 1 5n ∑ n = 1 ∞ b n = ∑ n = 1 ∞ 1 5 n which is a geometric series with r = 15 <1 r = 1 5 <1, and thus, converges. by the comparison test part (i), the series ∑∞ n=1 1 2 5n ∑ n = 1 ∞ 1 2 5 n converges as well. (b) to find bn b n, focus on both the numerator and the denominator of an a n to contruct an inequality. The limit comparison test: suppose an > 0 and bn > 0 for all n. if lim n→∞ the two series x an and x bn either both converge or both diverge. ∞ 1.
Ex Infinite Series Limit Comparison Test Radical Divergent Take bn = 1 5n b n = 1 5 n. the series ∑∞ n=1 bn = ∑∞ n=1 1 5n ∑ n = 1 ∞ b n = ∑ n = 1 ∞ 1 5 n which is a geometric series with r = 15 <1 r = 1 5 <1, and thus, converges. by the comparison test part (i), the series ∑∞ n=1 1 2 5n ∑ n = 1 ∞ 1 2 5 n converges as well. (b) to find bn b n, focus on both the numerator and the denominator of an a n to contruct an inequality. The limit comparison test: suppose an > 0 and bn > 0 for all n. if lim n→∞ the two series x an and x bn either both converge or both diverge. ∞ 1. We compare infinite series to each other using limits. using the comparison test can be hard, because finding the right sequence of inequalities is difficult. the limit comparison test eliminates this part of the method. if 0
Infinite Series The Limit Comparison Test Divergent Physics Forums We compare infinite series to each other using limits. using the comparison test can be hard, because finding the right sequence of inequalities is difficult. the limit comparison test eliminates this part of the method. if 0
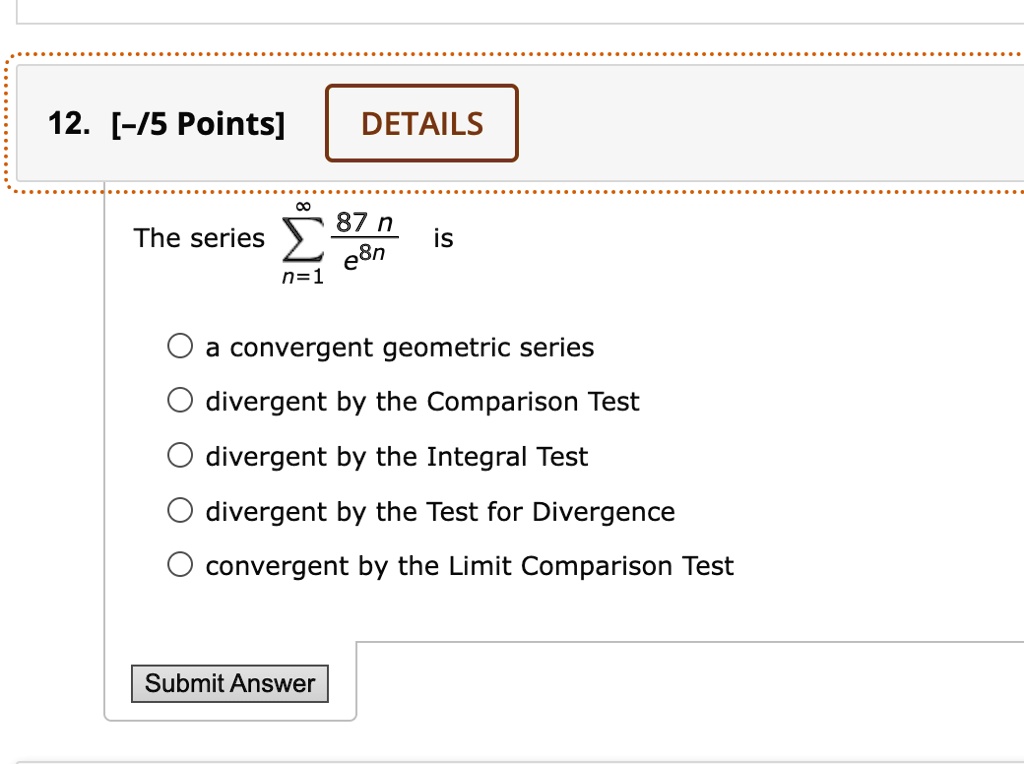
Solved 12 5 Points Details 87 N The Series Is E8n N 1 A Use the limit comparison test to show that a series is either convergent or divergent. suppose ∑ a n and ∑ b n are series with positive terms where: if 0
Comments are closed.