Evaluate Logarithm Expression Log1 3 81 Log1 3 9
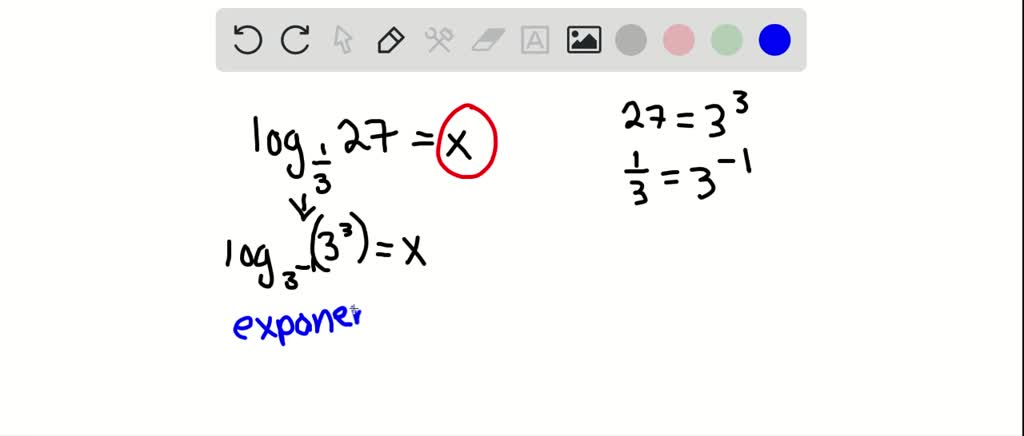
Solved Evaluate Each Logarithm Log1 3 27 Free logarithms calculator simplify logarithmic expressions using algebraic rules step by step. In this video, i share with you steps for using properties laws of logarithms to solve the problem. evaluate the logarithm expression log (1 3) (81) log (1 3.
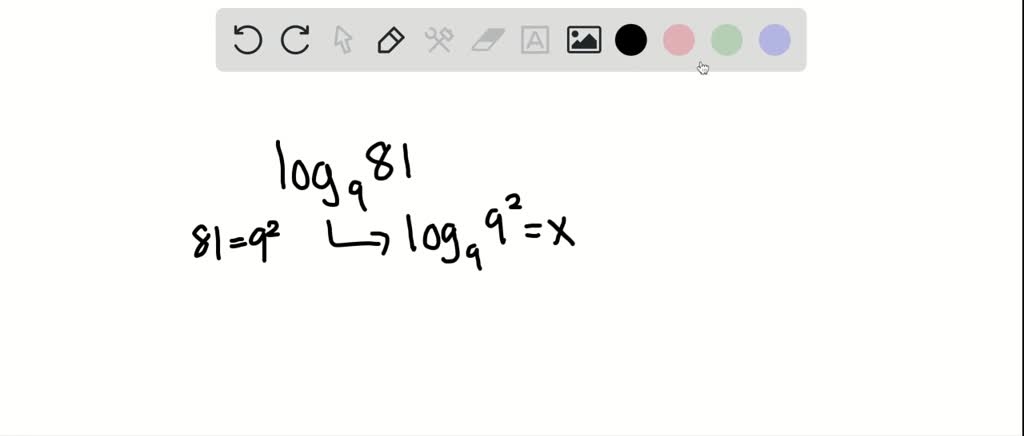
Solved Evaluate Each Logarithm Log9 81 Enter the logarithmic expression below which you want to simplify. the logarithm calculator simplifies the given logarithmic expression by using the laws of logarithms. click the blue arrow to submit. choose "simplify condense" from the topic selector and click to see the result in our algebra calculator! ln(e4.5) l n (e 4. 5). To evaluate log31 81, we start by letting x = log31 81. by definition of logarithms, this is equivalent to (31)x = 81. next, observe that the expression (31)x can be rewritten using properties of exponents. recall that 31 = 3−1, so (31)x = (3−1)x = 3−x. thus, our equation becomes 3−x = 81. now, notice that 81 is a power of 3, namely, 81. This free log calculator solves for the unknown portions of a logarithmic expression using base e, 2, 10, or any other desired base. Evaluate logarithms calculator online with solution and steps. detailed step by step solutions to your evaluate logarithms problems with our math solver and online calculator.
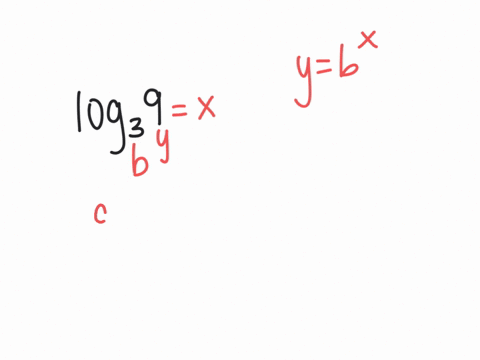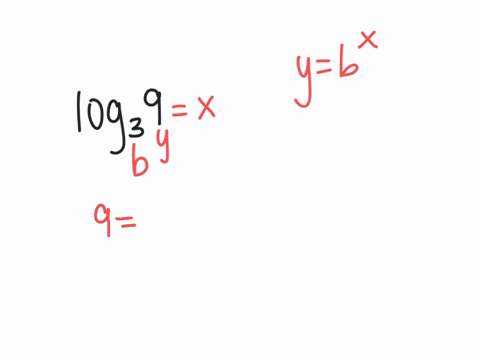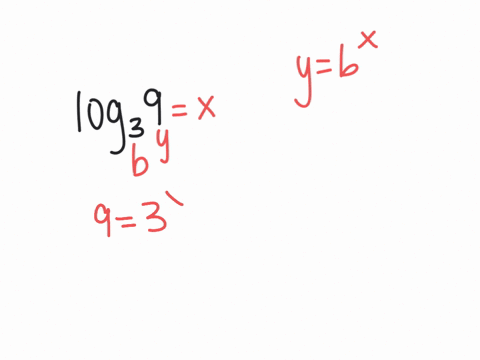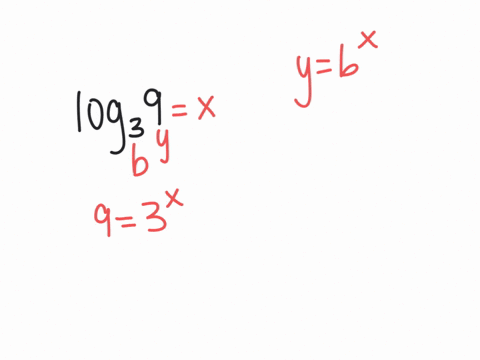
Solved Evaluate Each Logarithm Log3 9 This free log calculator solves for the unknown portions of a logarithmic expression using base e, 2, 10, or any other desired base. Evaluate logarithms calculator online with solution and steps. detailed step by step solutions to your evaluate logarithms problems with our math solver and online calculator. Estimate the value of logarithms and evaluate certain logarithms exactly without a calculator. before you get started, take this readiness quiz. 1. simplify (81−−√)2 (81) 2. 2. evaluate 23 2 3. 3. evaluate 3−2 3 2. 4. write 7–√3 7 3 using exponents. it works well to ‘undo’ an operation with another operation. Knowing the squares, cubes, and roots of numbers allows us to evaluate many logarithms mentally. for example, consider log28 l o g 2 8. we ask, “to what exponent must 2 be raised in order to get 8?” because we already know 23 =8 2 3 = 8, it follows that log28 =3 l o g 2 8 = 3. now consider solving log749 l o g 7 49 and log327 l o g 3 27 mentally. Rewrite log1 3 (81) = x log 1 3 (81) = x in exponential form using the definition of a logarithm. if x x and b b are positive real numbers and b b does not equal 1 1, then logb (x) = y log b (x) = y is equivalent to by = x b y = x. To solve a logarithmic equations use the esxponents rules to isolate logarithmic expressions with the same base. set the arguments equal to each other, solve the equation and check your answer.
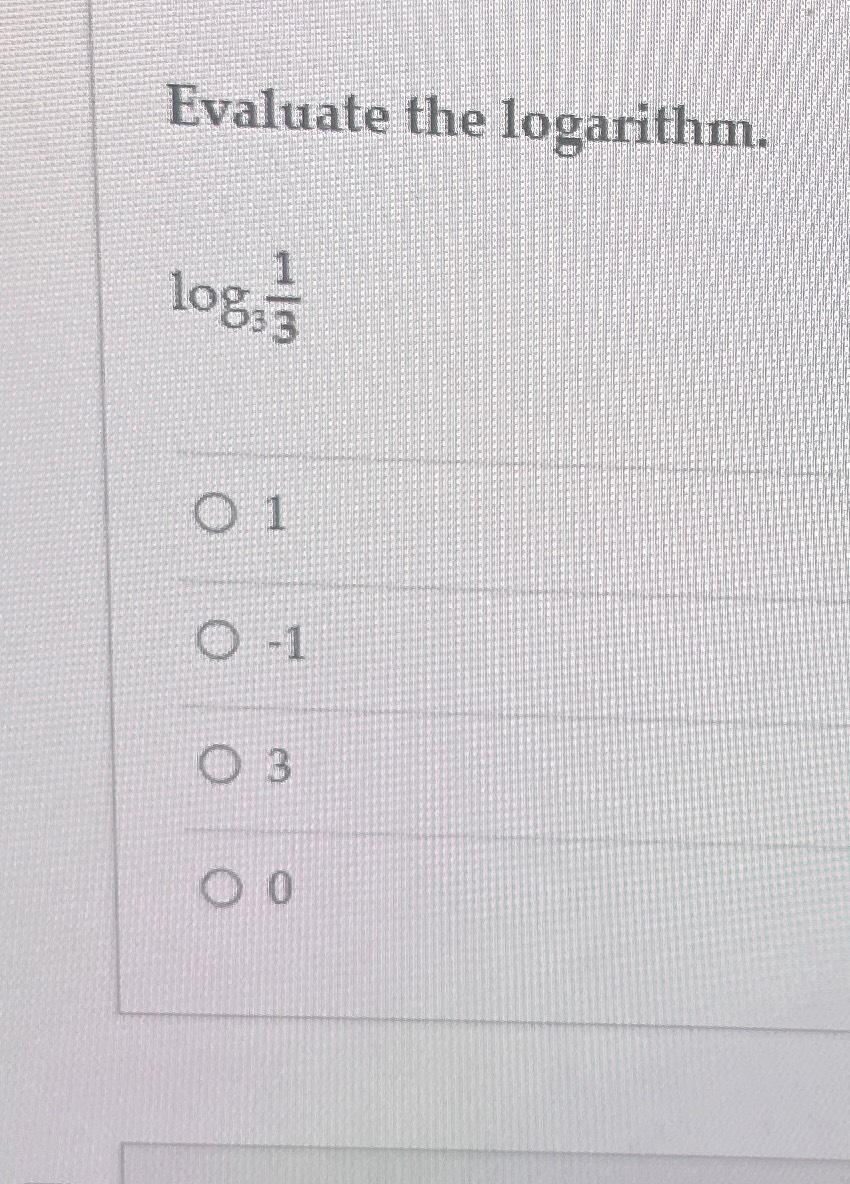
Solved Evaluate The Logarithm Log3131 130 Chegg Estimate the value of logarithms and evaluate certain logarithms exactly without a calculator. before you get started, take this readiness quiz. 1. simplify (81−−√)2 (81) 2. 2. evaluate 23 2 3. 3. evaluate 3−2 3 2. 4. write 7–√3 7 3 using exponents. it works well to ‘undo’ an operation with another operation. Knowing the squares, cubes, and roots of numbers allows us to evaluate many logarithms mentally. for example, consider log28 l o g 2 8. we ask, “to what exponent must 2 be raised in order to get 8?” because we already know 23 =8 2 3 = 8, it follows that log28 =3 l o g 2 8 = 3. now consider solving log749 l o g 7 49 and log327 l o g 3 27 mentally. Rewrite log1 3 (81) = x log 1 3 (81) = x in exponential form using the definition of a logarithm. if x x and b b are positive real numbers and b b does not equal 1 1, then logb (x) = y log b (x) = y is equivalent to by = x b y = x. To solve a logarithmic equations use the esxponents rules to isolate logarithmic expressions with the same base. set the arguments equal to each other, solve the equation and check your answer.
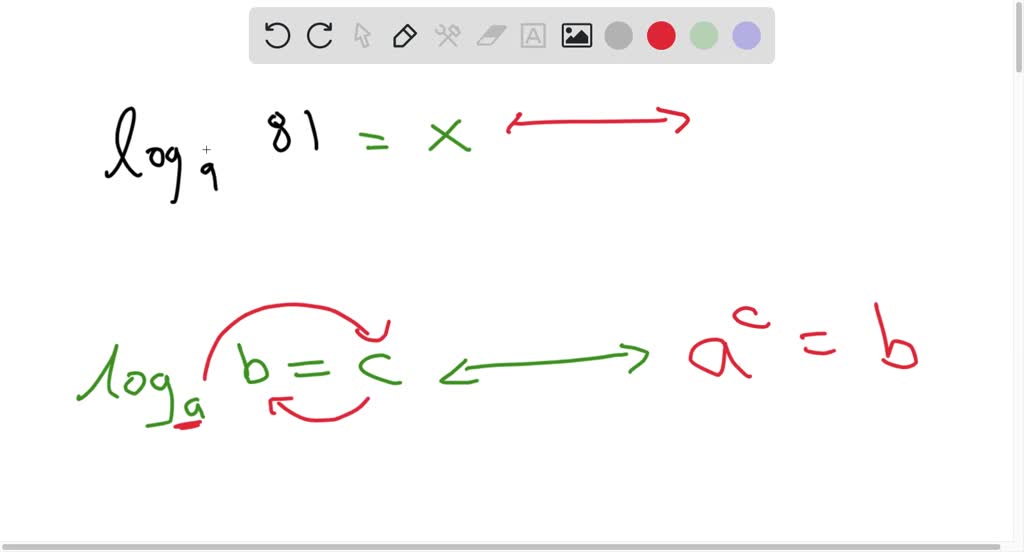
Solved Evaluate Each Logarithm Log9 81 Rewrite log1 3 (81) = x log 1 3 (81) = x in exponential form using the definition of a logarithm. if x x and b b are positive real numbers and b b does not equal 1 1, then logb (x) = y log b (x) = y is equivalent to by = x b y = x. To solve a logarithmic equations use the esxponents rules to isolate logarithmic expressions with the same base. set the arguments equal to each other, solve the equation and check your answer.

Answered Question 1 Evaluate The Logarithm Log1 30 3 Decimal Places
Comments are closed.