Euclidian Vector Spaces Linear Algebra Studocu
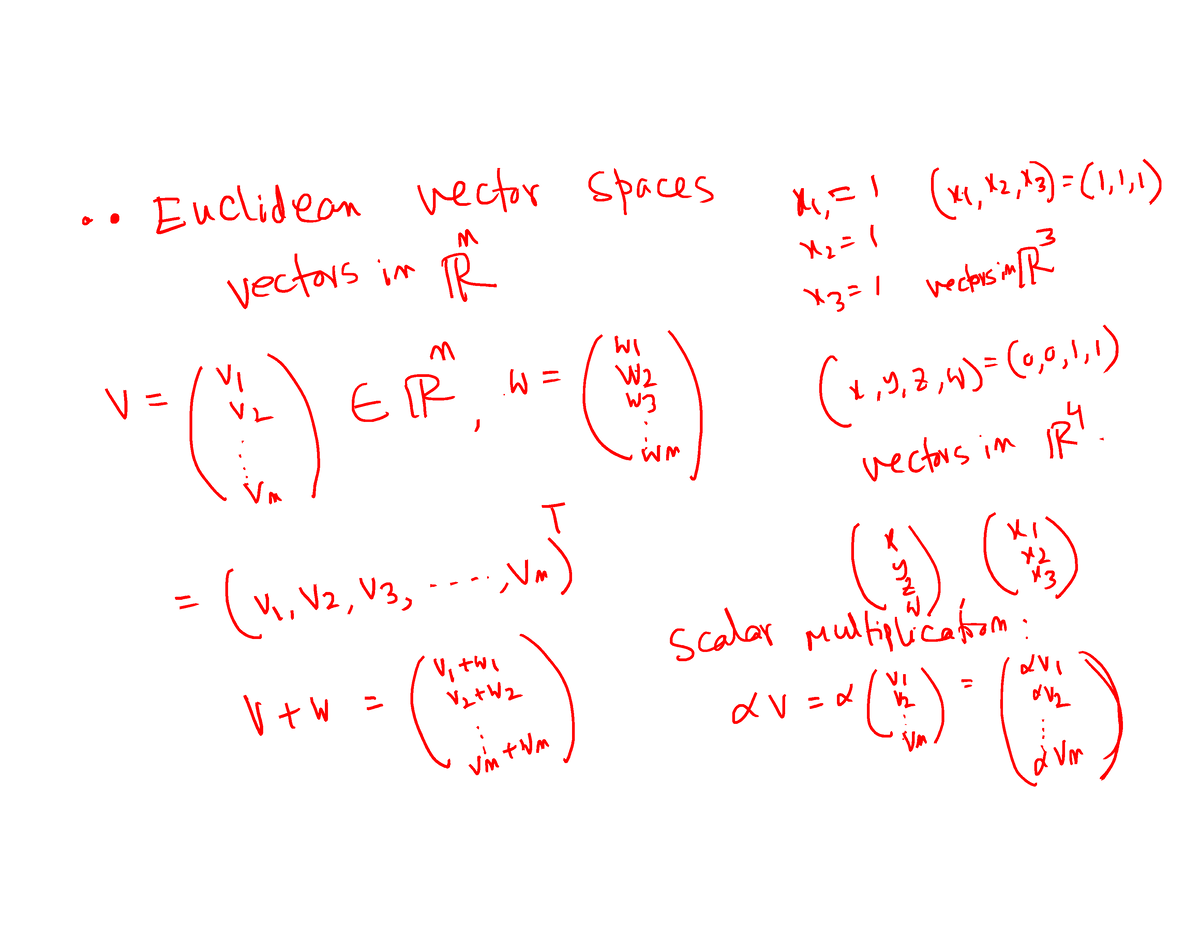
Euclidian Vector Spaces Linear Algebra Studocu Was this document helpful? on studocu you find all the lecture notes, summaries and study guides you need to pass your exams with better grades. When we want to indicate that a vector v has initial point a and terminal point b, then, as shown in figure 3.1, we will write ab 131132 chapter3 euclidean vector spaces b vectors with the same length and direction, such as those in figure 3.1, are said to be equivalent.

03 Euclidean Vector Spaces Pdf In this section we will review the basic properties of vectors in two and three dimensions with the goal of extending these properties to vectors in r n . Euclidean vector space is a type of vector space that is equipped with a notion of distance, known as the euclidean distance or the "length" of a vector. the standard examples of euclidean vector spaces are r^n, the n dimensional real space, and c^n, the n dimensional complex space. This chapter on euclidean vector spaces introduces fundamental concepts such as vector representation, vector arithmetic, dot products, and the properties of linear transformations. Let v be an euclidean space. for all v, w ∈ v we have | v, w | ≤ ∥v∥.∥w∥. furthermore, the equal ity holds if and only if u, v are linearly dependent. proof. if v, w are linearly dependent, then either v = λw or w = λv for some real number λ. without loss of generality, suppose that v = λw.

Lecture Notes Vector Spaces Mat 1033 Studocu This chapter on euclidean vector spaces introduces fundamental concepts such as vector representation, vector arithmetic, dot products, and the properties of linear transformations. Let v be an euclidean space. for all v, w ∈ v we have | v, w | ≤ ∥v∥.∥w∥. furthermore, the equal ity holds if and only if u, v are linearly dependent. proof. if v, w are linearly dependent, then either v = λw or w = λv for some real number λ. without loss of generality, suppose that v = λw. Find the equation of the plane: (a) through (1,2,3) and parallel to both u = (1, 1, 1) and v = (2, 3, 1) (in vector form) (b) through (1,2,3) and orthogonal to u = (1, 1, 1) (in general form) (c) through the points p (1, 2, 3), q (2, 2, 2), and r (3, 2, 0) (in parametric form). 1. experimental data a scientist performs an experiment and makes n numerical measurements each time the experiment is performed. the result of each experiment can be regarded as a vector y= (y1, y2, , yn) in r^n which y1, y2, , yn are the measured values. Mindful that majority of the students taking this module are new to the subject, we have chosen to introduce the concepts of linear algebra in the context of euclidean spaces rather than to jump straight into abstract vector spaces , which will be covered in the second course. Vectors in euclidean space linear algebra math 2010 • euclidean spaces: first, we will look at what is meant by the different euclidean spaces. – euclidean 1 space <1 : the set of all real numbers, i., the real line. for example, 1, 12 , 2 are all elements of <1 .

Lecture 01 Vector Spaces Optimization And Computational Linear Find the equation of the plane: (a) through (1,2,3) and parallel to both u = (1, 1, 1) and v = (2, 3, 1) (in vector form) (b) through (1,2,3) and orthogonal to u = (1, 1, 1) (in general form) (c) through the points p (1, 2, 3), q (2, 2, 2), and r (3, 2, 0) (in parametric form). 1. experimental data a scientist performs an experiment and makes n numerical measurements each time the experiment is performed. the result of each experiment can be regarded as a vector y= (y1, y2, , yn) in r^n which y1, y2, , yn are the measured values. Mindful that majority of the students taking this module are new to the subject, we have chosen to introduce the concepts of linear algebra in the context of euclidean spaces rather than to jump straight into abstract vector spaces , which will be covered in the second course. Vectors in euclidean space linear algebra math 2010 • euclidean spaces: first, we will look at what is meant by the different euclidean spaces. – euclidean 1 space <1 : the set of all real numbers, i., the real line. for example, 1, 12 , 2 are all elements of <1 .
Comments are closed.