Differential Equations Lecture 8 3 Predator Prey Models

Predator Prey Modelling Using Differential Equations Pdf Ecology In this lecture, we analyze two types of lotka volterra models of predator prey relationships. in the first, the prey grows exponentially without the predator, and in the second, the. Example 1 (cont.) there are two xed points of the following system, (x ;y ) = (0;0) and (3;2): (x0 = x(1 1 2y) y0 = 3 y( 4 1 x) 4.

Analyzing Predator Prey Models Using Systems Of Ordinary Linear D Pdf Modeling predator prey interactions the lotka volterra model is the simplest model of predator prey interactions. it was developed independently by: alfred lotka, an american biophysicist (1925), and vito volterra, an italian mathematician (1926). basic idea: population change of one species depends on: its current population. its reproduction. Use the preceding step to write a single differential equation for y as a function of x, with the time variable t eliminated from the problem. the solutions of this differential equation are called trajectories of the system. Nonlinear systems: predator–prey models. assumptionstwo species, one feeding on the other 1.prey population x(t); predator population y(t) 2.if no predators, prey population grows at natural rate: for some constant a > 0, dx dt = ax =)x(t) = x0eat. Keeping the assumptions of the basic model for a disease, write a pair autonomous differential equations to describe how both the proportion of infected individuals, i, and the proportion of susceptible individuals, s, change over time.

Solved Consider The Following Predator Prey System Of Differential Nonlinear systems: predator–prey models. assumptionstwo species, one feeding on the other 1.prey population x(t); predator population y(t) 2.if no predators, prey population grows at natural rate: for some constant a > 0, dx dt = ax =)x(t) = x0eat. Keeping the assumptions of the basic model for a disease, write a pair autonomous differential equations to describe how both the proportion of infected individuals, i, and the proportion of susceptible individuals, s, change over time. We will see that these models take the form of a pair of linked differential equations. we first consider the situation in which one species, called the prey, has an ample food supply and the second species, called the predators, feeds on the prey. Predator prey equations descriptions: the classic lotka volterra model of predator prey competition, which describes interactions between foxes and rabbits, or big fish and little fish, is the foundation of mathematical ecology. This example provides a basic introduction to the predator prey dynamics described by the lotka volterra equations. experiment with different parameters and initial conditions to observe the rich behavior of this classic model. Predator prey modeling solving ordinary differential equations predator prey model = number of rabbits.

Solved Consider The Following Pair Of Differential Equations Chegg We will see that these models take the form of a pair of linked differential equations. we first consider the situation in which one species, called the prey, has an ample food supply and the second species, called the predators, feeds on the prey. Predator prey equations descriptions: the classic lotka volterra model of predator prey competition, which describes interactions between foxes and rabbits, or big fish and little fish, is the foundation of mathematical ecology. This example provides a basic introduction to the predator prey dynamics described by the lotka volterra equations. experiment with different parameters and initial conditions to observe the rich behavior of this classic model. Predator prey modeling solving ordinary differential equations predator prey model = number of rabbits.
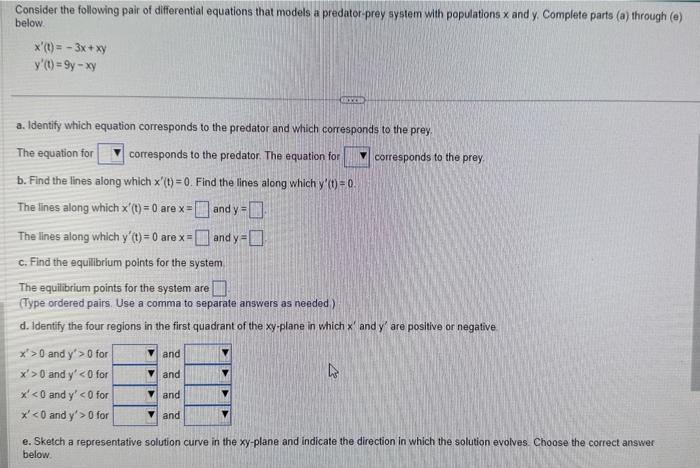
Solved Consider The Following Pair Of Differential Equations Chegg This example provides a basic introduction to the predator prey dynamics described by the lotka volterra equations. experiment with different parameters and initial conditions to observe the rich behavior of this classic model. Predator prey modeling solving ordinary differential equations predator prey model = number of rabbits.
Comments are closed.