Determining The Domain Of Bessel Function J1x

Bessel S Function R R N X X J Pdf Discrete Mathematics Number Theory Episode 000025saturday, september 28th, 2019we will be using the ratio test to determine domain of the bessel function j1 (x).textbook: "calculus: early trans. The bessel functions of the first kind j n (x) are defined as the solutions to the bessel differential equation x^2 (d^2y) (dx^2) x (dy) (dx) (x^2 n^2)y=0 (1) which are nonsingular at the origin.

Intermediate Physics For Medicine And Biology Integral Of The Bessel J nhpxl x figure 1: the bessel functions jn( x) for n = 0; 1; 2; 3 in trending from left to right, illustrating their oscillatory asymptotic character. to establish this more precisely, the integrand can be cast into complex exponential form, and the method of steepest descents performed when z 1 . A spherically symmetric square well potential in quantum mechanics is solved by spherical bessel functions. also, the extrac tion of phase shifts from atomic and nuclear scattering data requires spherical bessel functions. in sections 8.5 and 8.6 series solutions to bessel’s equation were developed. A ∞. finite domain in ρ, say 0 ≤ ρ ≤ a, we can determine a countable set of eigenvalues from the set of zeros of the bessel functions jm. if our domain in ρ becomes infinite, then we cannot determine the eigenvalues, and instead we have a continuous set. Solution of equation (1) when α = n. consider α = n ε 6∈z corresponding bessel equation has two independent solutions jn ε and j (n ε). − the function yn ε defined by jn ε(x) ( 1)nj (n ε)(x) yn ε(x) = − − − . ε since function yn ε is a linear combination of jn ε and solution of the corresponding bessel’s equation of order.
Solved The Domain Of The Bessel Function Of Order 0 Defined By J 0 X A ∞. finite domain in ρ, say 0 ≤ ρ ≤ a, we can determine a countable set of eigenvalues from the set of zeros of the bessel functions jm. if our domain in ρ becomes infinite, then we cannot determine the eigenvalues, and instead we have a continuous set. Solution of equation (1) when α = n. consider α = n ε 6∈z corresponding bessel equation has two independent solutions jn ε and j (n ε). − the function yn ε defined by jn ε(x) ( 1)nj (n ε)(x) yn ε(x) = − − − . ε since function yn ε is a linear combination of jn ε and solution of the corresponding bessel’s equation of order. Jp(x) is called the bessel function of the first kind of order p. a second linearly independent solution can be found via reduction of order. when (appropriately normalized), it is denoted by yp(x), and is called the bessel function of the second kind of order p. y = c1jp(x) c2yp(x). bessely(p,x). Bessel functions 1. bessel function j ode representation (y(x j x is a solution to this ode) ) = n( ) x2y xy x2 n2 y. Are you using the taylor series definition of the bessel function? if so, then write out some terms and think where it might be undefined and what it's radius of convergence is. Question: j1, the bessel function of order 1, is defined byj1=∑n=0∞ ( 1)nx2n 1n! (n 1)!22n 1find the domain of j1. find the domain of j 1. there are 2 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly.
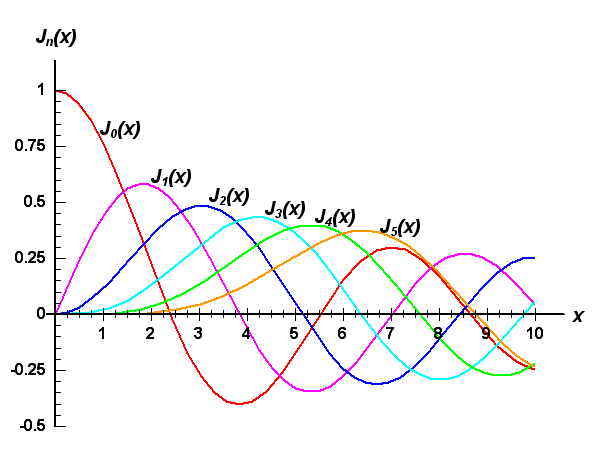
Dplot Besselj Function Jp(x) is called the bessel function of the first kind of order p. a second linearly independent solution can be found via reduction of order. when (appropriately normalized), it is denoted by yp(x), and is called the bessel function of the second kind of order p. y = c1jp(x) c2yp(x). bessely(p,x). Bessel functions 1. bessel function j ode representation (y(x j x is a solution to this ode) ) = n( ) x2y xy x2 n2 y. Are you using the taylor series definition of the bessel function? if so, then write out some terms and think where it might be undefined and what it's radius of convergence is. Question: j1, the bessel function of order 1, is defined byj1=∑n=0∞ ( 1)nx2n 1n! (n 1)!22n 1find the domain of j1. find the domain of j 1. there are 2 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly.

Solved Question 1 20 Marks Expand The Following Function In A Are you using the taylor series definition of the bessel function? if so, then write out some terms and think where it might be undefined and what it's radius of convergence is. Question: j1, the bessel function of order 1, is defined byj1=∑n=0∞ ( 1)nx2n 1n! (n 1)!22n 1find the domain of j1. find the domain of j 1. there are 2 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly.
Comments are closed.