Derivatives Of Vector Functions

Derivatives Of Vector Functions Pdf Calculate the derivative of a vector valued function by taking the derivative of the components of the vector functions. differentiate each of the components of the vector function. apply the derivative rules we’ve learned in the past to simplify the derivative of the components. Given a real valued function f (x), we know that the derivative of f at x = a represents the slope of the line tangent to f at the point (a; f (a)). what can we say about the derivative of a vector valued function #r (t)? graphical interpretation, cont. recall that for a vector function #r (t), we have: #r (t h) #r 0(t) = lim h!0 h.

Unit 4 Pt 2 Pt 2 Derivatives Vector Functions Pdf The purpose of this document is to help you learn to take derivatives of vectors, matrices, and higher order tensors (arrays with three dimensions or more), and to help you take derivatives with respect to vectors, matrices, and higher order tensors. The derivative of a vector valued function can be understood to be an instantaneous rate of change as well; for example, when the function represents the position of an object at a given point in time, the derivative represents its velocity at that same point in time. In this section here we discuss how to do basic calculus, i.e. limits, derivatives and integrals, with vector functions. Derivative of an n dimensional vector function a function f of a real number t with values in the space can be written as . its derivative equals f ′ ( t ) = ( f 1 ′ ( t ) , f 2 ′ ( t ) , … , f n ′ ( t ) ) {\displaystyle f' (t)= (f {1}' (t),f {2}' (t),\ldots ,f {n}' (t))} .

Derivative And Integral Vector Functions Pdf In this section here we discuss how to do basic calculus, i.e. limits, derivatives and integrals, with vector functions. Derivative of an n dimensional vector function a function f of a real number t with values in the space can be written as . its derivative equals f ′ ( t ) = ( f 1 ′ ( t ) , f 2 ′ ( t ) , … , f n ′ ( t ) ) {\displaystyle f' (t)= (f {1}' (t),f {2}' (t),\ldots ,f {n}' (t))} . Peed is simply the absolute value of the deriva. ive. but to motion along a curve in a plane or in space. assume that a curve in the plane is parameter. zed as hx(t); y(t)i or, in space, by hx(t); y(t); z(t)i. let p = p (t) be the point corresponding to t, which we may think of as \t. sition vector, r = r(t). What does the derivative of a vector valued function measure? what do we mean by the integral of a vector valued function and how do we compute it? how do we describe the motion of a projectile if the only force acting on the object is acceleration due to gravity?. Learn how to calculate derivatives and integrals of vector functions so we can define motion along a curve in a plane or space.
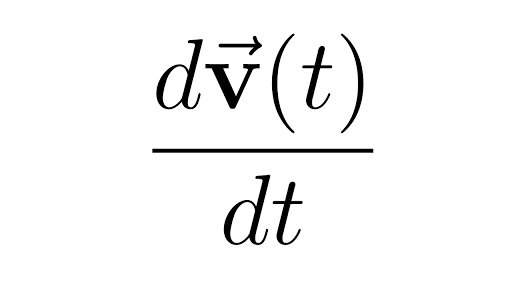
Derivatives Of Vector Valued Functions Article Khan Academy Peed is simply the absolute value of the deriva. ive. but to motion along a curve in a plane or in space. assume that a curve in the plane is parameter. zed as hx(t); y(t)i or, in space, by hx(t); y(t); z(t)i. let p = p (t) be the point corresponding to t, which we may think of as \t. sition vector, r = r(t). What does the derivative of a vector valued function measure? what do we mean by the integral of a vector valued function and how do we compute it? how do we describe the motion of a projectile if the only force acting on the object is acceleration due to gravity?. Learn how to calculate derivatives and integrals of vector functions so we can define motion along a curve in a plane or space.

Solution Derivatives Of Vector Functions Studypool Learn how to calculate derivatives and integrals of vector functions so we can define motion along a curve in a plane or space.
Comments are closed.