Derivative Of A Vector Function Of A Scalar Variable Engineering

1 1 Vector Calculus Derivative Of Scalar Vector Function Pdf Write an expression for the derivative of a vector valued function. find the tangent vector at a point for a given position vector. find the unit tangent vector at a point for a given position vector and explain its significance. calculate the definite integral of a vector valued function. Consider a vector valued function of a scalar, for example the time dependent displacement of a particle u u (t ) . in this case, the derivative is defined in the usual way, partial derivatives can also be defined in the usual way. for example, if u is a function of the coordinates, u ( x. 0.

Vector Function With Respect To Scalar Variable Pdf Derivative A vector function r (t)= f (t),g (t),h (t) is a function of one variable. what makes vector functions more complicated than the functions y=f (x). the values are now three dimensional vectors instead of simply numbers. it is natural to wonder if there is a corresponding notion of derivative for vector functions. one way to approach the question of. Given a real valued function f (x), we know that the derivative of f at x = a represents the slope of the line tangent to f at the point (a; f (a)). what can we say about the derivative of a vector valued function #r (t)? graphical interpretation, cont. recall that for a vector function #r (t), we have: #r (t h) #r 0(t) = lim h!0 h. The partial derivative of a vector function a with respect to a scalar variable q is defined as ∂ a ∂ q = ∑ i = 1 n ∂ a i ∂ q e i {\displaystyle {\frac {\partial \mathbf {a} } {\partial q}}=\sum {i=1}^ {n} {\frac {\partial a {i}} {\partial q}}\mathbf {e} {i}}. The purpose of this document is to help you learn to take derivatives of vectors, matrices, and higher order tensors (arrays with three dimensions or more), and to help you take derivatives with respect to vectors, matrices, and higher order tensors.

Derivative And Integral Vector Functions Pdf The partial derivative of a vector function a with respect to a scalar variable q is defined as ∂ a ∂ q = ∑ i = 1 n ∂ a i ∂ q e i {\displaystyle {\frac {\partial \mathbf {a} } {\partial q}}=\sum {i=1}^ {n} {\frac {\partial a {i}} {\partial q}}\mathbf {e} {i}}. The purpose of this document is to help you learn to take derivatives of vectors, matrices, and higher order tensors (arrays with three dimensions or more), and to help you take derivatives with respect to vectors, matrices, and higher order tensors. Partial derivatives of vectors. if a is a vector depending on more than one scalar variable (x, y, z), then we write a = a(x, y, z). the partial derivative of a with respect to x, y and. Mple, f(x; y) = x2 xy y3 and f(x; y; z) = [xyz; y3z y2]. if a scalar function f takes d real values as its input, we say that f is a scalar eld in rd. similarly, if a ector function f takes d f is a vector eld in rd. for example, the f(x; y) and f(x; y; z) shown earlier are a scalar eld in r2 and a vector eld in r3, respectively. What are vector valued functions? a vector valued function is any function that returns multiple values (outputs). these are quite common in engineering models; rarely do we only care about scalar inputs and scalar outputs to a model. here are some examples of vector valued functions in the wild:. The derivative of a vector function is a vector containing the derivatives of each component function. it measures the rate of change of the vector with respect to a scalar variable, such as time or distance.
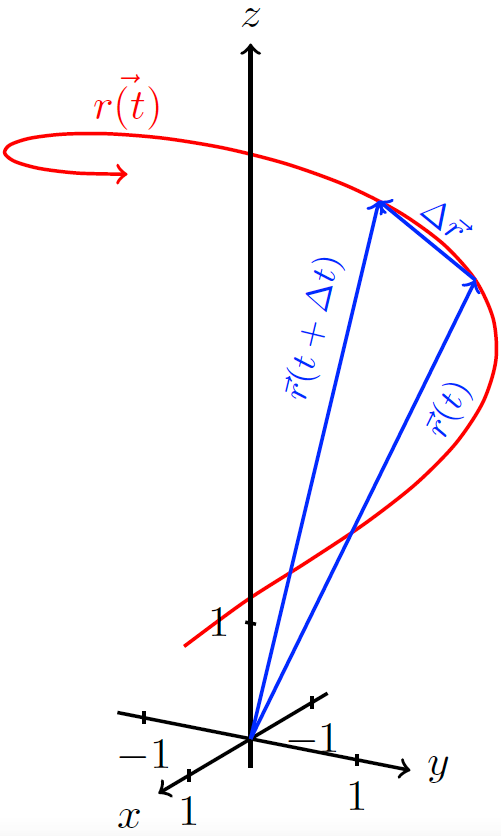
Derivative Vector Function Tikz Net Partial derivatives of vectors. if a is a vector depending on more than one scalar variable (x, y, z), then we write a = a(x, y, z). the partial derivative of a with respect to x, y and. Mple, f(x; y) = x2 xy y3 and f(x; y; z) = [xyz; y3z y2]. if a scalar function f takes d real values as its input, we say that f is a scalar eld in rd. similarly, if a ector function f takes d f is a vector eld in rd. for example, the f(x; y) and f(x; y; z) shown earlier are a scalar eld in r2 and a vector eld in r3, respectively. What are vector valued functions? a vector valued function is any function that returns multiple values (outputs). these are quite common in engineering models; rarely do we only care about scalar inputs and scalar outputs to a model. here are some examples of vector valued functions in the wild:. The derivative of a vector function is a vector containing the derivatives of each component function. it measures the rate of change of the vector with respect to a scalar variable, such as time or distance.
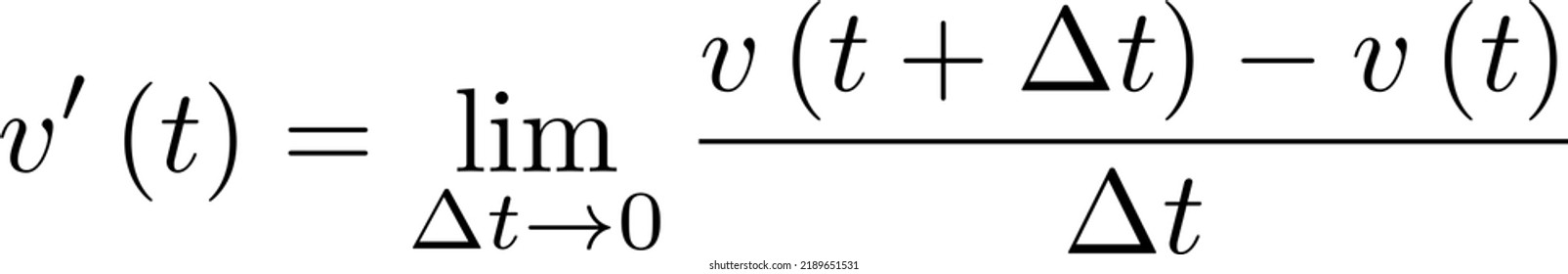
Derivative Vector Function Stock Vector Royalty Free 2189651531 What are vector valued functions? a vector valued function is any function that returns multiple values (outputs). these are quite common in engineering models; rarely do we only care about scalar inputs and scalar outputs to a model. here are some examples of vector valued functions in the wild:. The derivative of a vector function is a vector containing the derivatives of each component function. it measures the rate of change of the vector with respect to a scalar variable, such as time or distance.
Comments are closed.