Continuous Deployment For Windows Containers With Github Actions Deploy

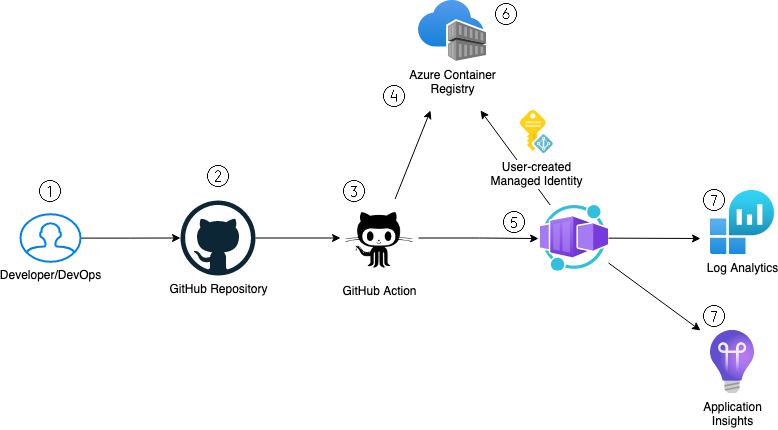
Continuous Deployment For Windows Containers With Github Actions Deploy The continuous extension of f(x) f (x) at x = c x = c makes the function continuous at that point. can you elaborate some more? i wasn't able to find very much on "continuous extension" throughout the web. how can you turn a point of discontinuity into a point of continuity? how is the function being "extended" into continuity? thank you. Following is the formula to calculate continuous compounding a = p e^(rt) continuous compound interest formula where, p = principal amount (initial investment) r = annual interest rate (as a.

Continuous Deployment Fundamentals With Github Actions Resources Hub A continuous function is a function where the limit exists everywhere, and the function at those points is defined to be the same as the limit. i was looking at the image of a piecewise continuous. @user1742188 it follows from heine cantor theorem, that a continuous function over a compact set (in the case of , compact sets are closed and bounded) is uniformly continuous. 6 all metric spaces are hausdorff. given a continuous bijection between a compact space and a hausdorff space the map is a homeomorphism. proof: we show that f f is a closed map. let k ⊂e1 k ⊂ e 1 be closed then it is compact so f(k) f (k) is compact and compact subsets of hausdorff spaces are closed. hence, we have that f f is a homeomorphism. Closure of continuous image of closure ask question asked 12 years, 8 months ago modified 12 years, 8 months ago.

Github 0anastasia Continuousdeployment 6 all metric spaces are hausdorff. given a continuous bijection between a compact space and a hausdorff space the map is a homeomorphism. proof: we show that f f is a closed map. let k ⊂e1 k ⊂ e 1 be closed then it is compact so f(k) f (k) is compact and compact subsets of hausdorff spaces are closed. hence, we have that f f is a homeomorphism. Closure of continuous image of closure ask question asked 12 years, 8 months ago modified 12 years, 8 months ago. If it is k k times differentiable and that k k th derivative is continuous, one writes f ∈ck(x, y). f ∈ c k (x, y) i don't think there is a common notation for a function which is differentiable, but whose derivative is not continuous. Then f f is continuous if and only if f(a¯¯¯¯) ⊆f(a)¯ ¯¯¯¯¯¯¯¯¯ f (a) ⊆ f (a), where a¯¯¯¯ a denotes the closure of an arbitrary set a a. assuming f f is continuous, the result is almost immediate. perhaps i am missing something obvious, but i have not been able to make progress on the other direction. You'll find topological properties with indication of whether they are preserved by (various kinds of) continuous maps or not (such as open maps, closed maps, quotient maps, perfect maps, etc.). for mere continuous most things have been mentioned: simple covering properties (variations on compactness, connectedness, lindelöf) and separability. Now my question is, is this a continuous determination of the argument or if no could you help me do define the argument continuously and maybe give some reference where to find it?.

Github Storemyprojects Github Actions Continuous Delivery Azure If it is k k times differentiable and that k k th derivative is continuous, one writes f ∈ck(x, y). f ∈ c k (x, y) i don't think there is a common notation for a function which is differentiable, but whose derivative is not continuous. Then f f is continuous if and only if f(a¯¯¯¯) ⊆f(a)¯ ¯¯¯¯¯¯¯¯¯ f (a) ⊆ f (a), where a¯¯¯¯ a denotes the closure of an arbitrary set a a. assuming f f is continuous, the result is almost immediate. perhaps i am missing something obvious, but i have not been able to make progress on the other direction. You'll find topological properties with indication of whether they are preserved by (various kinds of) continuous maps or not (such as open maps, closed maps, quotient maps, perfect maps, etc.). for mere continuous most things have been mentioned: simple covering properties (variations on compactness, connectedness, lindelöf) and separability. Now my question is, is this a continuous determination of the argument or if no could you help me do define the argument continuously and maybe give some reference where to find it?.

Continuous Deployment Using Github Actions Smartscribs You'll find topological properties with indication of whether they are preserved by (various kinds of) continuous maps or not (such as open maps, closed maps, quotient maps, perfect maps, etc.). for mere continuous most things have been mentioned: simple covering properties (variations on compactness, connectedness, lindelöf) and separability. Now my question is, is this a continuous determination of the argument or if no could you help me do define the argument continuously and maybe give some reference where to find it?.

Automate Your Deployment With Github Actions