Building Recurrence Relations From Recursive Code Exercise Design And Analysis Of Algorithms

Analysis Of Recursive Algorithms Pdf Recurrence Relation Logic In this video i show how you can build a recurrence relation that expresses the runtime of some recursive code. In this article, we will learn about the basics of recurrence relations and how to analyze them. what is recurrence relation? a recurrence relation is a mathematical expression that defines a sequence in terms of its previous terms. in the context of algorithmic analysis, it is often used to model the time complexity of recursive algorithms.

Recurrence Relation For Complexity Analysis Of Algorithms Pdf Time Evaluating an algorithm? use asymptotic analysis. evaluating an implementation? timing can be useful. example: compute something recursively on a list of size n. conceptually, in each recursive call we: when do we hit the base case? when n k = 0! what about a binary version of sum? can we get a binarysearch like runtime?. In my algorithm and data structures class we were given a few recurrence relations either to solve or that we can see the complexity of an algorithm. at first, i thought that the mere purpose of these relations is to jot down the complexity of a recursive divide and conquer algorithm. Our approach to the analysis of recursive algorithms differs somewhat. the first three steps are the same: determining the input size parameter, identifying the basic operation, and separating best, average, and worst case behavior. This version of power does work. what is the recurrence relation that describes its running time? long power(long x, long n) if (n==0) return 1; if (n==1) return x; if ((n % 2) == 0) return power(x,n 2) * power(x,n 2); else return power(x,n.2) * power(x,n 2) * x; (0) t = c.

Recurrence Relation Of Recursive Algorithms Made Easy Lec 20 Our approach to the analysis of recursive algorithms differs somewhat. the first three steps are the same: determining the input size parameter, identifying the basic operation, and separating best, average, and worst case behavior. This version of power does work. what is the recurrence relation that describes its running time? long power(long x, long n) if (n==0) return 1; if (n==1) return x; if ((n % 2) == 0) return power(x,n 2) * power(x,n 2); else return power(x,n.2) * power(x,n 2) * x; (0) t = c. A recurrence relation, t(n), is a recursive function of integer variable n. like all recursive functions, it has both recursive case and base case. example: the portion of the definition that does not contain t is called the base case of the recurrence relation; the portion that contains t is called the recurrent or recursive case. Ction of the entire set of recursive invocations of the function t. the goal of drawing a recursion tree is to obtain a guess hich can then be verified by the more rigorous substitution method. iteration is an algebraic version of the recursion tree method, and consists of repeatedly substituting the recu. How to solve recurrence relations? f ang . a recurrence relation defines each term of a sequence using preceding term(s), and always state the initial term of the sequence. recurrence relation captures the dependence of a term to its preceding terms. solution. given recurrence relation for a sequence. When we analyze the complexity of a recursive algorithm, we obtain a recurrence relation that expresses the number of operations required to solve a problem of size n in terms of the number of operations required to solve the problem for one or more instance of smaller size.

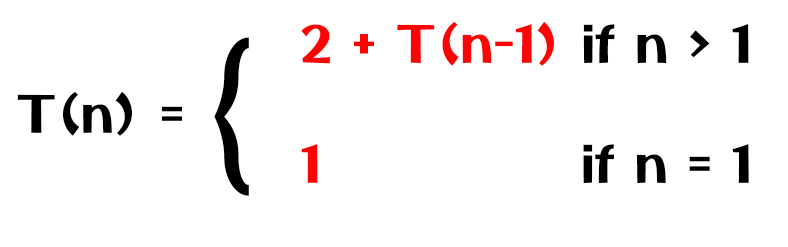
Recurrence Relation Of Recursive Algorithms Made Easy Lec 20 A recurrence relation, t(n), is a recursive function of integer variable n. like all recursive functions, it has both recursive case and base case. example: the portion of the definition that does not contain t is called the base case of the recurrence relation; the portion that contains t is called the recurrent or recursive case. Ction of the entire set of recursive invocations of the function t. the goal of drawing a recursion tree is to obtain a guess hich can then be verified by the more rigorous substitution method. iteration is an algebraic version of the recursion tree method, and consists of repeatedly substituting the recu. How to solve recurrence relations? f ang . a recurrence relation defines each term of a sequence using preceding term(s), and always state the initial term of the sequence. recurrence relation captures the dependence of a term to its preceding terms. solution. given recurrence relation for a sequence. When we analyze the complexity of a recursive algorithm, we obtain a recurrence relation that expresses the number of operations required to solve a problem of size n in terms of the number of operations required to solve the problem for one or more instance of smaller size.