Bessel Function Problem 7 Bessel Function Engineering Mathematics 3

Bessel Functions Pdf Abstract Algebra Calculus Subject engineering mathematics 3video name bessel function problem 7chapter bessel functionfaculty prof. farhan meerupskill and get placements with. To satisfy the boundary conditions (3), (4), we plug z = 0 or z = h and use fourier bessel formulas. which is formula (29) in the handout \bessel functions".

Bessel Functions Pdf Mathematics Mathematical Analysis 12.2 bessel’s equation the differential equation 1 is known as bessel’s equation of order lutions are called bessel’s functions. series solut n of 1 in terms o and is given by where. Bessel functions of the rst and second kind are the most commonly found forms of the bessel function in ap plications. many applications in hydrodynamics, elastic ity, and oscillatory systems have solutions that are based on the bessel functions. We start our detailed study of bessel functions by introducing a generating function yield ing the jn for integer n (of either sign). Watch and learn bessel function problem 7 from engineering mathematics 3 in instrumentation engineering with ekeeda. this video provides you with a detailed understanding of bessel function problem 7.

Bessel Functions Review Pdf Differential Equations Ordinary We start our detailed study of bessel functions by introducing a generating function yield ing the jn for integer n (of either sign). Watch and learn bessel function problem 7 from engineering mathematics 3 in instrumentation engineering with ekeeda. this video provides you with a detailed understanding of bessel function problem 7. Problems in cylindrical coordi nates. first we define another important function: the gamma function which is used in the series expansion of the bessel functions, then we const. uc. the bessel functi. function defined f. x > 0 by Γ(x) = e− ssx − 1ds . 0 the improper integra. defining Γ is convergent for x > 0. to see why, t for eve. Summary of bessel functions bessel’s equation 2 d 2 y dy 2 2 ) y = 0 . x x x − n dx 2 dx if n is an integer, the two independent solutions of bessel’s equation are • j ( x n ) , bessel function of the first kind, ∑ ∞ ( p 2 p n. Plots of the bessel functions j0(x),j1(x),j2(x) j 0 (x), j 1 (x), j 2 (x), and j3(x) j 3 (x). a second linearly independent solution is obtained for p p not an integer as j−p(x) j − p (x). Summary so far we solved bessel's equation: x2y00 xy0 (x2 found two generalized power series solutions: 2)y = 0, using the frobenius method, and 1 y1(x) x = x anxn;.

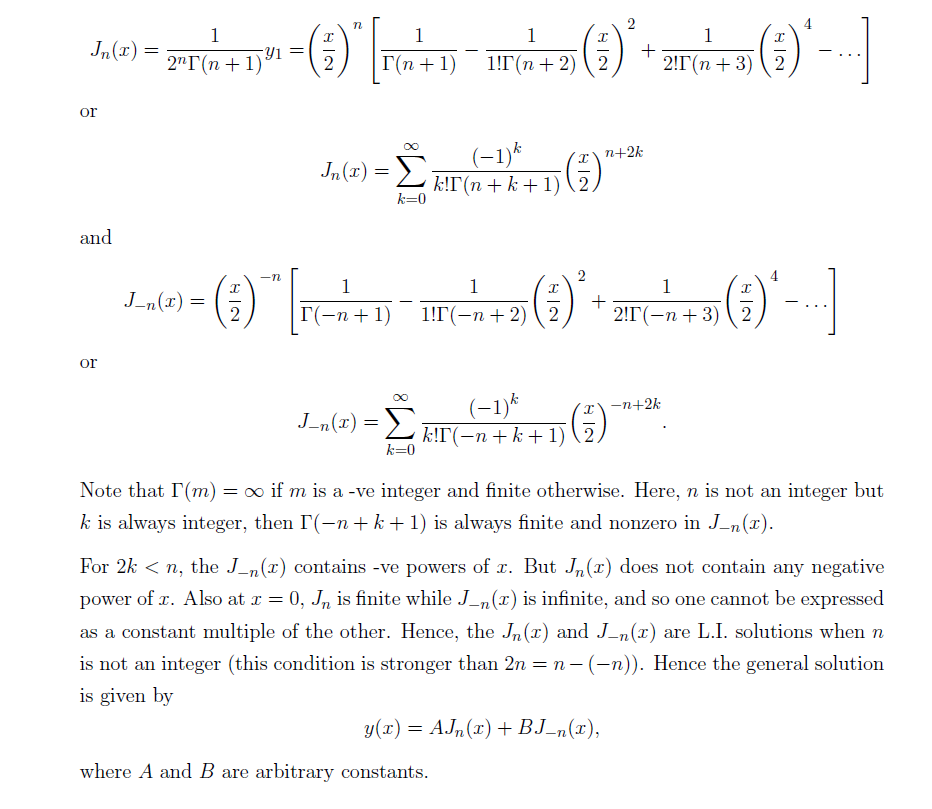
Bessel S Function Soul Of Mathematics Problems in cylindrical coordi nates. first we define another important function: the gamma function which is used in the series expansion of the bessel functions, then we const. uc. the bessel functi. function defined f. x > 0 by Γ(x) = e− ssx − 1ds . 0 the improper integra. defining Γ is convergent for x > 0. to see why, t for eve. Summary of bessel functions bessel’s equation 2 d 2 y dy 2 2 ) y = 0 . x x x − n dx 2 dx if n is an integer, the two independent solutions of bessel’s equation are • j ( x n ) , bessel function of the first kind, ∑ ∞ ( p 2 p n. Plots of the bessel functions j0(x),j1(x),j2(x) j 0 (x), j 1 (x), j 2 (x), and j3(x) j 3 (x). a second linearly independent solution is obtained for p p not an integer as j−p(x) j − p (x). Summary so far we solved bessel's equation: x2y00 xy0 (x2 found two generalized power series solutions: 2)y = 0, using the frobenius method, and 1 y1(x) x = x anxn;.

Unit 3 Bessel Functions Pdf Recurrence Relation Diffraction Plots of the bessel functions j0(x),j1(x),j2(x) j 0 (x), j 1 (x), j 2 (x), and j3(x) j 3 (x). a second linearly independent solution is obtained for p p not an integer as j−p(x) j − p (x). Summary so far we solved bessel's equation: x2y00 xy0 (x2 found two generalized power series solutions: 2)y = 0, using the frobenius method, and 1 y1(x) x = x anxn;.