Answered Consider The Following Series N 1 Use The Limit Comparison

Answered Consider The Following Series N 1 Use The Limit Comparison Our expert help has broken down your problem into an easy to learn solution you can count on. there are 2 steps to solve this one. the given series is, ∑ n = 1 ∞ sin (1 n). not the question you’re looking for? post any question and get expert help quickly. In this section we will discuss using the comparison test and limit comparison tests to determine if an infinite series converges or diverges. in order to use either test the terms of the infinite series must be positive. proofs for both tests are also given.

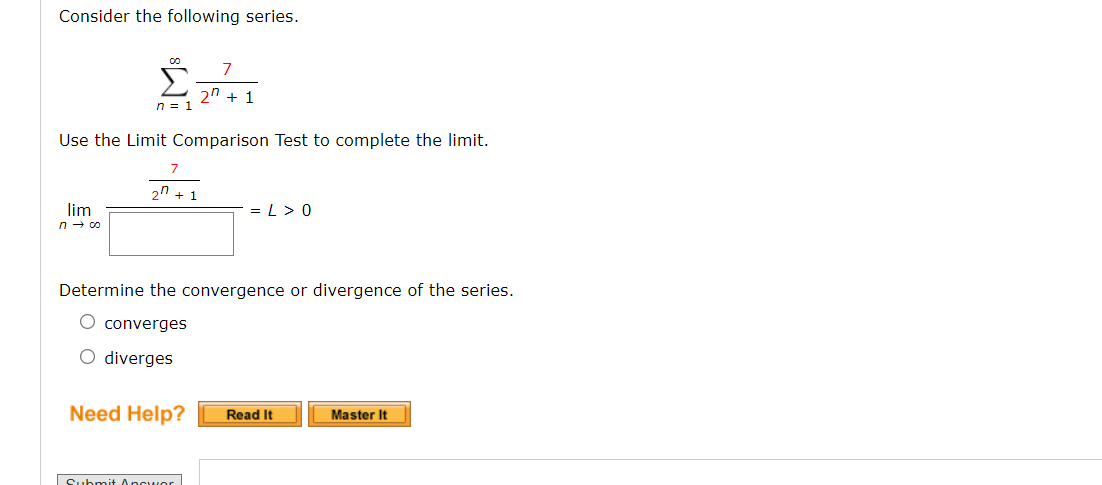
Solved Consider The Following Series в N 1в ћ72n 1use The Limit Chegg To determine the convergence or divergence of the series ∑n=1∞ tan(n1), we can use the limit comparison test. here's a step by step explanation: as a comparison series. the harmonic series is a well known divergent series. Basic answer ### ideas for solving the problem 1. **limit comparison test:** the limit comparison test states that if we have two series $\sum a n$ and $\sum b n$ with positive terms, and $\lim {n \to \infty} \frac {a n} {b n} = l$, where $0 < l < \infty$, then both series either converge or both diverge. 2. The comparison test works nicely if we can find a comparable series satisfying the hypothesis of the test. however, sometimes finding an appropriate series can be difficult. consider the series ∞ ∑ n=2 1 n2 −1 ∑ n = 2 ∞ 1 n 2 1. Step 1 1) comparision test: let ∑ n = 1 ∞ a n and ∑ n = 1 ∞ b n be a series with positive terms. suppose, view the full answer step 2.

Solved Consider The Following Series в N 1в ћn 2 в 1 N 1 Find Chegg The comparison test works nicely if we can find a comparable series satisfying the hypothesis of the test. however, sometimes finding an appropriate series can be difficult. consider the series ∞ ∑ n=2 1 n2 −1 ∑ n = 2 ∞ 1 n 2 1. Step 1 1) comparision test: let ∑ n = 1 ∞ a n and ∑ n = 1 ∞ b n be a series with positive terms. suppose, view the full answer step 2. To determine the convergence or divergence of the series , we can use the limit comparison test. this test helps us compare our given series with a known benchmark series to determine its convergence behavior. Choosing an appropriate comparison series is crucial for the success of the limit comparison test. in this case, $\sum \frac {1} {n^4}$ was a good choice because it has a similar form to the given series and its convergence is easily determined. remember to check that the limit $\lim {n \to \infty} \frac {a n} {b n}$ is a positive finite. ∑ n = 1 ∞ t a n (1 n) use the limit comparison test to complete the limit lim n → ∞ t a n (1 n) = l> 0. Using the limit comparison test, the series ∑n=1∞ n n8 11 converges, as it compares favorably with the convergent p series ∑n=1∞ n51. the positive limit we calculated confirms this. therefore, the answer is a. converges. to determine whether the series ∑n=1∞ nn8 1 1 converges or diverges, we can use the limit comparison test.

Solved Consider The Following Series в N 1в ћen в 1 N Find The Chegg To determine the convergence or divergence of the series , we can use the limit comparison test. this test helps us compare our given series with a known benchmark series to determine its convergence behavior. Choosing an appropriate comparison series is crucial for the success of the limit comparison test. in this case, $\sum \frac {1} {n^4}$ was a good choice because it has a similar form to the given series and its convergence is easily determined. remember to check that the limit $\lim {n \to \infty} \frac {a n} {b n}$ is a positive finite. ∑ n = 1 ∞ t a n (1 n) use the limit comparison test to complete the limit lim n → ∞ t a n (1 n) = l> 0. Using the limit comparison test, the series ∑n=1∞ n n8 11 converges, as it compares favorably with the convergent p series ∑n=1∞ n51. the positive limit we calculated confirms this. therefore, the answer is a. converges. to determine whether the series ∑n=1∞ nn8 1 1 converges or diverges, we can use the limit comparison test.

Solved Consider The Following Series в N 1в ћn2 3 в 1 N 1n2 Chegg ∑ n = 1 ∞ t a n (1 n) use the limit comparison test to complete the limit lim n → ∞ t a n (1 n) = l> 0. Using the limit comparison test, the series ∑n=1∞ n n8 11 converges, as it compares favorably with the convergent p series ∑n=1∞ n51. the positive limit we calculated confirms this. therefore, the answer is a. converges. to determine whether the series ∑n=1∞ nn8 1 1 converges or diverges, we can use the limit comparison test.

Solved Consider The Following Series в N 1в ћn 8 в 1 N 1 Find Chegg