Analysis Points Are Expanded In A Three Dimensional Coordinate System

Analysis Points Are Expanded In A Three Dimensional Coordinate System The graph of a function of two variables, say, z = f(x, y) z = f (x, y), lies in euclidean space, which in the cartesian coordinate system consists of all ordered triples of real numbers (a, b, c) (a, b, c). since euclidean space is 3 dimensional, we denote it by r3 r 3. We’ll start the chapter off with a fairly short discussion introducing the 3 d coordinate system and the conventions that we’ll be using. we will also take a brief look at how the different coordinate systems can change the graph of an equation.

Three Dimensional Coordinate System Stable Diffusion Online Download scientific diagram | analysis points are expanded in a three dimensional coordinate system from publication: study on the mechanism affecting the quality of. We have given a one to one correspondence between points p in space and ordered triplets (a, b, c) in r3. it is called a tree dimensional rectangular coordinate system. The cylindrical coordinate system is a coordinate system that essentially extends the two dimensional polar coordinate system by adding a third coordinate measuring the height of a point above the plane, similar to the way in which the cartesian coordinate system is extended into three dimensions. To identify a point in the plane, we use its cartesian (or rectangular) coordinates. that is, we identify each point in p ∈ r2 using the notation p (x, y) or simply (x, y). in this course we will also be working with the three dimensional analogue of the plane, r3 or three space.

Three Dimensional Coordinate System Stable Diffusion Online The cylindrical coordinate system is a coordinate system that essentially extends the two dimensional polar coordinate system by adding a third coordinate measuring the height of a point above the plane, similar to the way in which the cartesian coordinate system is extended into three dimensions. To identify a point in the plane, we use its cartesian (or rectangular) coordinates. that is, we identify each point in p ∈ r2 using the notation p (x, y) or simply (x, y). in this course we will also be working with the three dimensional analogue of the plane, r3 or three space. Section 12.1 three dimensional coordinate systems goals: plot points in a three dimensional coordinate system. use the distance formula. recognize the equation of a sphere and nd its radius and center. graph an implicit function with a free variable. Three dimensional coordinate system. functions of two variables. surfaces from two to three dimensions. a point in the two dimensional coordinate system is represented by an ordered pair (x; y): there are 2 coordinate axis, x and y; which divide the plane into 4 quadrants. To describe a point in three dimensional space, we need three numbers or an ordered triple (a; b; c). the point (a; b; c) means a point that is a units in the x direction, b units in the y direction, and c units in the z direction (see figure 2).

Three Dimensional Coordinate System Stable Diffusion Online Section 12.1 three dimensional coordinate systems goals: plot points in a three dimensional coordinate system. use the distance formula. recognize the equation of a sphere and nd its radius and center. graph an implicit function with a free variable. Three dimensional coordinate system. functions of two variables. surfaces from two to three dimensions. a point in the two dimensional coordinate system is represented by an ordered pair (x; y): there are 2 coordinate axis, x and y; which divide the plane into 4 quadrants. To describe a point in three dimensional space, we need three numbers or an ordered triple (a; b; c). the point (a; b; c) means a point that is a units in the x direction, b units in the y direction, and c units in the z direction (see figure 2).

Coordinate System For Three Dimensional Measurement System Download To describe a point in three dimensional space, we need three numbers or an ordered triple (a; b; c). the point (a; b; c) means a point that is a units in the x direction, b units in the y direction, and c units in the z direction (see figure 2).

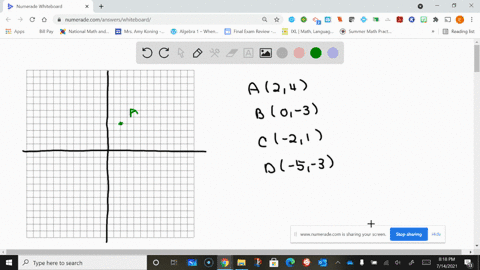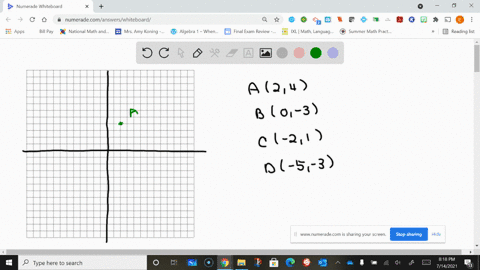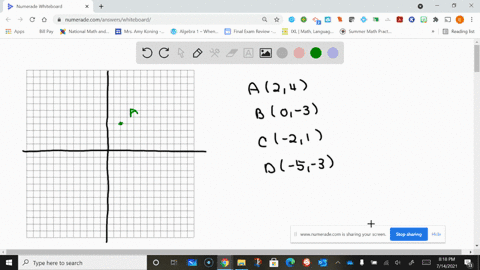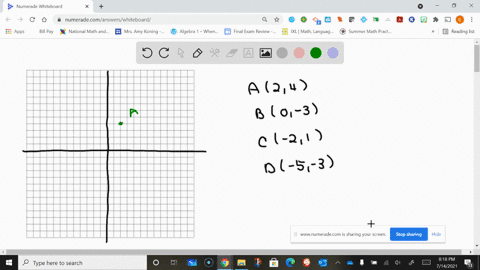
Solved Plot The Given Points In A Three Dimensional Coordinate System